Relatività B, A.A. 2009-10:
Introduzione alla fisica dei Buchi Neri

1. 23-11-09:
   Presentazione del corso. Motiviazioni ed obiettivi. Testi e materiale bibliografico on-line. La fisica dei buchi neri nel contesto attuale della Fisica Teorica.
2. 23-11-09 :
   Introduzione storica. Gli ``astri occulti'' di Michell e Laplace. Il `` raggio gravitazionale critico''.
   

3. 25-11-09 :
   Eserc.
   1. 1) Calcolare l'area della sezione 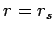$r=r_s$ della metrica di Schwarzschild.
   2. 2) Calcolare il "tempo di volo" di un fotone, emesso radialmente in 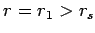$r=r_1>r_s$, al tempo 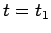$t=t_1$, e ricevuto in 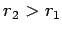$r_2>r_1$ al tempo 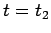$t=t_2$. Cosa succede nel limite $r_1\to r_s$ ?
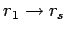   3. 3) Calcolare il red-shift del fotone in $2)$
   4. 4) Determinare l' andamento della luminosità di una stella quando il suo raggio si avvicina a $r_s$.
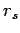   5. 5) Calcolare il ``tempo proprio'' di caduta, radiale, da 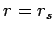$r=r_s$ a $r=0$.
4. 25-11-09 :
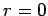   Eserc. Determinare la forma esplicita di un sistema di coordinate localmente inerziali nella metrica di Schwarzschild.
   In questo sistema di riferimento calcolare $R^0_{r0r}$.
5. 26-11-09 :
   La curvatura dell' orizzonte: tensore di Riemann e Scalare di Kreshmann. Singolarità di Curvatura e Singolarità di Coordinate.
6. 26-11-09 :
   La metrica di Rindler. Curvatura ed orizzonte.
   Continuazione analitica a tempo immaginario.
   Temperatura del vuoto di Rindler.
7. 30-11-09 :
   Eserc. Effetto Unruh. Temperatura di Rindler per un elettrone accelerato a $10^{26}\, m/s^2$.
   Determinare la Near-horizon geometry di un buco nero di Schwarzschild.
8. 30-11-09 :
   La Temperatura di un buco nero (Hawking, 1974).
   La ``Prima Legge della Termodinamica'' per un buco nero. L' Entropia termodinamica di un buco nero.
9. 02-12-09 :
   Entropia ``statistica'' e numero di microstati di un buco-nero.
   ``Principio Olografico'' (cenni).
10. 02-12-09 :
    Struttura dei coni-luce, nella metrica di Schwartzschild. Coordinate di Eddington-Finkelstein e Kruskal-Szekeres. Metrica di Schwartzschild in coordinate di Kruskal-Szekeres.
11. 03-12-09 :
    Il Diagramma di Kruskal. Buchi Neri e Buchi Bianchi. Orizzonti di eventi futuri e passati. Massima estensione analitica della metrica di Schwartzschild.
12. 03-12-09 :
    Geometria (qualitativa) delle sezioni $x^0=cost.$ della metrica di Schwartzschild in coordinate di Kruskal.
    Il ``Ponte di Einstein-Rosen'' come esempio di ``wormhole non-attraversabile''.
13. 09-12-09 :
    Eserc.
    • Ricavare il Diagramma di Penrose per la metrica di Minkowski
    • Costruire la massima estensione analitica della metrica di Rindler
    • Ricavare il Diagramma di Penrose per la metrica di Rindler
    • Ricavare il Diagramma di Penrose per la metrica di Schwarzschild
14. 09-12-09 :
    Eserc.
    • Ricavare il Diagramma di Penrose per la metrica di Schwarzschild all'esterno di una stella stazionaria
    • Ricavare il Diagramma di Penrose per la metrica di Schwarzschild all'esterno di una stella che collassa in un buco nero
    • Rappresentare mediante diagrammi di Penrose i possibili stati finali dell' evaporazione di un mini-buco nero
15. 10-12-09 :
    Eserc. Verificare che $\partial_{[\mu}\, A_{\nu]}\equiv \nabla_{[\mu}\, A_{\nu]}$.
    Calcolare la forma generale del tensore energia-impulso del campo eletromagnetico partendo dall' azione di Maxwell covariante.
    Determinare le componenti non-nulle del tensore energia-impulso per un campo elettrico radiale.
16. 10-12-09 :
    La soluzione di Reissner-Nordström delle equazioni di Einstein. Orizzonti e singolarità di curvatura.
17. 14-12-09 :
    Condizione di esistenza degli orizzonti, $G_N M^2> Q^2$: significato geometrico; interpretazione classica in termini di energia gravitazionale di legame ed energia coulombiana.
    Studio dell'equazione degli orizzonti.
18. 14-12-09 :
    Eserc. Costruire il diagramma di Penrose per la metrica di Reissner-Nordström con due orizzonti; adattare il diagramma al caso del collasso di una sfera carica.
19. 16-12-09 :
    Eserc. Studiare, qualitativamente, l'evoluzione della metrica di una sfera di materia carica in collasso, disegnando sezioni a tempo costante della geometria.
    Ricavare near-horizon geometry per un buco nero di Reissner-Nordström. Determinare la gravità di superficie e la temperatura dell' orizzonte.
20. 16-12-09 :
    Eserc. Studiare l'anadamento della temperatura di Hawking in funzione del raggio dell' orizzonte.
    Ricavare l'entropia del buco nero dalla prima legge della termodinamica e verificare che: i) è un quarto dell'area; ii) è zero nel caso estremale.
21. 17-12-09 :
    Introduzione alla metrica di Kerr: evidenze fenomenologiche vs ``patologie'' geometriche.
    Risolvere l'equazione di campo debole
    

    $$\partial^2\, \phi^{\mu\nu}=\kappa\, T^{\mu\nu}$$ (1)

    
    
    per una sfera di materia lentamente ruotante.
22. 17-12-09 :
    Eserc. Dimostrare che per una distribuzione di materia , sferica, statica, nel limite di campo debole, la condizione

    
    

    $$\partial_\mu T^{\mu\nu}=0$$ (2)

    
    

    comporta che

    
    

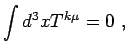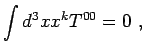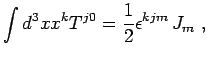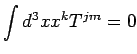    $$\int d^3x T^{k\mu}=0\ ,$$

    $$\int d^3x x^k T^{00}=0\ ,$$

    $$\int d^3x x^k T^{j0}=\frac{1}{2}\epsilon^{kjm}\, J_m\ ,$$

    $$\int d^3x x^k T^{jm}=0$$ (3)

    
    

23. 11-01-10 :
    La metrica di Kerr in coordinate di Boyer-Lindquist.
    Significato geometrico delle coordinate. La singolarità anulare di curvatura. La metrica sul disco $x^2+y^2=a^2$. Significato fisico di $M$ ed $a$: confronto con la metrica della sfera lentamente ruotante.
24. 11-01-10 :
    Orizzonti di eventi e Superfici di red-shift infinito.
    Estrazione di energia: il ``processo di Penrose''.
    Velocità angolare dell'orizzonte di eventi.