- 01-03-2016:
Presentazione del corso:
obiettivi e contenuti. Pre-requisiti. Testi di
riferimento. Modalità di svolgimento dell'esame.
- 03-03-2016 :
La meccanica Newtoniana come teoria fenomenologica del moto a bassa velocità.
Non-covarianza delle equazioni di Newton e `` forze inerziali ''.
- 02-03-2016 :
Vincoli geometrici e vincoli cinematici. Vincoli cinematici integrabili e non-integrabili.
Sistemi olonomi e sistemi non-olonomi. Gradi di libertà. Spazio delle configurazioni.
- 02-03-2016:
Es. Esempi di sistemi con vincoli. Si consideri un sistema di due particelle 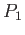 e
e 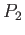 . La particella
. La particella 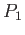 è
vincolata a muoversi lungo l'asse
è
vincolata a muoversi lungo l'asse 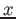 . La particella
. La particella 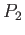 e collegata alla particella
e collegata alla particella 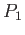 da una sbarra rigida di lunghezza
da una sbarra rigida di lunghezza 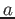 , di massa trascurabile.
i) Conteggiare il numero di gradi di libertà.
ii Determinare un possibile sistema di coordinate generalizzate.
, di massa trascurabile.
i) Conteggiare il numero di gradi di libertà.
ii Determinare un possibile sistema di coordinate generalizzate.
Si consideri un cilindro che rotola, (senza strisciare), su un piano inclinato.
Dimostrare che il vincolo di rotolamento è integrabile e determinare il numero di gradi
di libertà.
Si consideri una ruota che rotola su un piano perpendicolare alla ruota
stessa: non-integrabilità del vincolo cinematico.
- 04-03-2016:
Energia cinetica nello spazio delle configurazioni. Esempio: energia cinetica per il sistema di due particelle 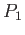 e
e 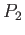 in cui
la particella
in cui
la particella 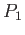 è
vincolata a muoversi lungo l'asse
è
vincolata a muoversi lungo l'asse 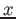 . La particella
. La particella 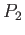 e collegata alla particella
e collegata alla particella 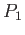 da una sbarra rigida di lunghezza
da una sbarra rigida di lunghezza 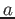 , di massa trascurabile.
, di massa trascurabile.
Momenti e forze generalizzate. Esempio: la forza peso generalizzata che agisce su un pendolo.
- 04-03-2016:
Equazioni di Lagrange come equazioni di Newton nello spazio delle configurazioni. La ``Lagrangiana'' per
un sistema conservativo. Esempio: equazioni di Lagrange per una particella di massa 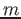 in un potenziale
in un potenziale
 .
.
- 08-03-2016
Es.
Descrizione Lagrangiana del moto di una particella in un campo di forze centrali. Conservazione del momento angolare.
Potenziale efficace per il problema radiale equivalente.
- 08-03-2016
Coordinate cicliche e costanti del moto. Non-unicità della Lagrangiana.
Potenziali dipendenti dalle velocità.
- 09-03-2016
Es.
Particella in moto libero sul piano in coordinate polari.
Particella carica in un campo eletro-magnetico esterno. Lagrangiana, equazioni del moto, energia totale del sistema.
Particella in caduta lungo una spira rotante. Lagrangiana equazioni, del moto, energia totale del sistema.
- 09-03-2016
Definizione generale di energia per un sistema Lagrangiano autonomo. Esempi: particella in un campo di forze
conservative; particella carica in un campo eletro-magnetico esterno; particella in caduta libera lungo
una spira circolare rotante a velocità angolare costante.
- 11-03-2016
Lo spazio delle fasi per un oscillatore armonico e per una particella in un potenziale parabolico repulsivo.
Orbite e punti fissi.
- 11-03-2016
Lo spazio delle fasi per il pendolo. Orbite e punti fissi.
- 15-03-2016
Oscillatore armonico smorzato. Caso di ``smorzamento forte''. Spazio delle fasi e punti fissi:
``nodo stabile
- 15-03-2016
Oscillatore armonico smorzato. Caso di ``smorzamento debole''. Spazio delle fasi e punti fissi:
``spirale stabile''. Caso di ``smorzamento debole''. Spazio delle fasi e punti fissi.
- 16-03-2016
Moltiplicatori di Lagrange. Esempi di moto vincolato lungo linee e superfici. Reazioni vincolari.
- 16-03-2016
Problema dei due-corpi in un campo di forze centrali. Separazione del moto del centro di massa
e del moto relativo.
- 18-03-2016
Equazioni del moto. Potenziale efficace e classificazione delle possibili orbite. Orbite nello spazio
delle fasi. La II Legge di Keplero.
- 18-03-2016
I Legge di Keplero: orbite come sezioni coniche. Eccentricità in funzione dell'energia. Orbite ellittiche.
III Legge di Keplero: periodo di rivoluzione.
- 21-03-2016
Correzioni al potenziale Newtoniano efficace e precessione del perielio di Mercurio.
- 21-03-2016
Cinematica del ``corpo rigido'' . Sistemi di riferimento inerziale e proprio.
Velocità ed energia cinetica totale. Il ``tensore d' inerzia''.
- 23-03-2016
Relazione tra il momento angolare del corpo rigido ed il tensore di inerzia. Momenti e prodotti
d' inerzia. Assi principali. Teorema dell asse parallelo (Teor. di Steiner)
- 23-03-2016
Es.
Dato il tensore d'inerzia:
![\begin{displaymath}
I^{mn}= m a^2 \,\left(\,
\begin{array}[c]{lll}
2 & 1 & 0\\
1 & 2 & 0\\
0 & 0 & 4
\end{array}\,\right)
\end{displaymath}](img7.png) |
(1) |
trovare i momenti d'inerzia e gli assi principali.
Data una sbarra omogenea di lunghezza 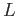 e dimensioni trasverse trascurabili,
determinare
e dimensioni trasverse trascurabili,
determinare 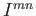 ripetto il punto medio della sbarra.
ripetto il punto medio della sbarra.
- 30-03-2016
Es
Data una sbarra omogenea di lunghezza 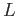 e dimensioni trasverse trascurabili,
determinare
e dimensioni trasverse trascurabili,
determinare 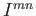 : a) rispetto un' estremità della sbarra; b) verificare
il Teorema di Steiner.
: a) rispetto un' estremità della sbarra; b) verificare
il Teorema di Steiner.
Dato un disco omogeneo calcolare 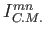 ed
ed 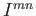 rispetto un sistema di assi
traslati parallelamente sulla circonferenza. Verificare che anche in entrambi i casi
rispetto un sistema di assi
traslati parallelamente sulla circonferenza. Verificare che anche in entrambi i casi
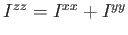 .
.
- 30-03-2016
Teorema dell'asse perpendicolare.
Gli angoli di Eulero.
- 01-04-2016
Velocità angolare ed energia cinetica del corpo rotante in funzione degli angoli di Eulero.
La Lagrangiana della ``trottola simmetrica''. Coordinate cicliche e costanti del moto.
- 01-04-2016
Es Dimostrare che la linea piu` corta tra due punti nel piano cartesiano e` la retta
che li unisce. Procedere cercando un ``estremo'' della lunghezza di una curva generica tra i due punti.
- 05-04-2016
Es.
Il problema della ``brachistocrona''.
Ricavare la Legge di Snell dal Principio (variazionale) di Fermat.
- 05-04-2016
Il calcolo delle variazioni: funzionali e derivate funzionali. Principio di ``minima azione'' secondo Maupertuis.
- 06-04-2016
Principio di ``minima azione'' di Hamilton: equazioni di Lagrange, e traiettorie classiche, come estremali, dell' azione.
Variazione ad ``estremi fissi''. Calcolo esplicito dell'azione per una particella libera. Derivazione variazionale
del moto di una carica in un campo elettrico e magnetico esterno.
- 06-04-2016
Trasformazioni di simmetria e variazione on-shell dell' azione.
Il Teorema di Emi Noether: le ``cariche di Noether''.
- 07-04-2016
Es Calcolare le cariche di Nother associate a simmetria per: i) traslazioni spaziali; ii) rotazioni; iii)
traslazioni nel tempo.
- 07-04-2016
Le equazioni di Hamilton.
Es Calcolare l' Hamiltoniana per: i) particella libera in un campo di forze conservative; ii)
una carica in un campo elettrico e campo magnetico esterni.
La Trasfomata di Legendre. Analogie tra ottica e meccanica nel formalismo Hamiltoniano.
- 12-04-2016
Equazioni di Hamilton da un principio variazionale. Conservazione dell'energia nel formalismo Hamiltoniano.
Lo spazio delle fasi come ``fluido incompressibile''.
- 12-04-2016
La parentesi di Poisson: definizione e proprietà.
Es
Dimostrare che le equazioni di Hamilton si possono scrivere come:
Calcolare :
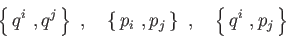 |
(2) |
Dimostrare che
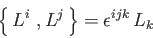 |
(3) |
- 13-04-2016
Es
Ricordando il teorema di E. Noether, dimstrare che :
per traslazioni spaziali
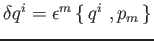 ;
;
per rotazioni
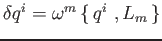 ;
;
per traslazioni nel tempo
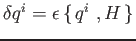 .
.
- 13-04-2016
Trasformazioni Canoniche. Invarianza della matrice simplettica e della parentesi di Poisson. Funzione genratrice.
L' evoluzione di un sistema come trasformazione canonica gnerata dall' Hamiltoniana.
Es Dato un oscillatore armonico in una dimensione, dimostrare che la trasformazione
| |
|
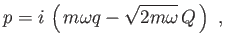 |
(4) |
| |
|
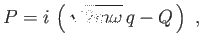 |
(5) |
è canonica. Trovare la funzione generatrice. Scrivere l' Hamiltoniana come funzione di 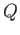 e
e 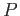 .
.
- 15-04-2016
L' azione come funzione dell'estremità finale della traiettoria.
Il principio variazionale di Jacobi.
- 15-04-2016
L' equazione di Hamilton-Jacobi.
Es.
Risolvere l'eq. di H-J neo caso della particella libera.
- 19-04-2016
La radiazione di ``corpo-nero''. Radianza spettrale e densità di energia per intervallo di frequenza.
- 19-04-2016
Es. Ricavare la legge di Rayleigh-Jeans assumento che il corpo nero e` una ``scatola'' cubica
metallica: calcolare il numero di onde stazionarie per intervallo di frequenza, ed utilizzare
di seguito il teorema classico di equipartizione dell'energia. La ``catastrofe ultra-violetta''.
- 20-04-2016
Es. Calcolare
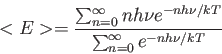 |
(6) |
Discutere i limiti di alta e bassa frequenza della densità di energia di corpo-nero.
- 20-04-2016
L' effetto foto-elettrico: la luce come fascio di ``fotoni''.
la diffusione di raggi-x da parte di eletroni: la spiegazione di Compton (cenni)
- 22-04-2016
I postulati di Bohr. Il modello semi-classico dell'atomo di Idrogeno.
Spettro dei livelli enegetici.
- 22-04-2016
Es. Dimostrare che  , e
, e 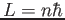 , sono casi particolari della regola di quantizzazione
di Wilson-Sommerfeld
, sono casi particolari della regola di quantizzazione
di Wilson-Sommerfeld
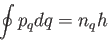 |
(7) |
L' ipotesi di De Broglie.
- 26-04-2016
L'esperimento di diffrazione di elettroni attraverso una doppia fenditura (Davisson-Germer). Il ``dualismo onda-corpuscolo''.
L' interpretazione di Born della ``funzione d'onda''.
- 26-04-2016
Es
Esprimere l' intensità di 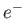 che arrivano sul sistema di rivelazione nell' esperimento di Davisson-Germer:
che arrivano sul sistema di rivelazione nell' esperimento di Davisson-Germer:
a) come intensità di un' onda
b) come intensità di un fascio di corpuscoli
c) dal confronto ricavare il sisgnificato statistico di
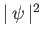
- 27-04-2016
L' equazione di Schrödinger. L'equazione di continuità per la corrente di probabilità.
- 27-04-2016
L' equazione di Schrödinger stazionaria come equazione agli auto-valori per l'energia.
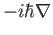 come ``operatore momento'',
come ``operatore momento'',
 come ``operatore energia''.
L' operatore Hamiltoniano.
come ``operatore energia''.
L' operatore Hamiltoniano.
- 29-04-2016
Risolvere L' equazione di Schrödinger , in una dimensione, per una particella libera col metodo di Fourier.
``Pacchetti d'onda''. Velocità di gruppo e velocità di fase.
- 29-04-2016
Es
Dato lo stato iniziale:
calcolare al tempo 
- il coefficiente di normalizzazione
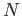
- i valori medi:
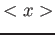 ,
, 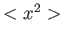 ,
, 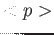 ,
, 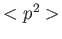
- verificare che
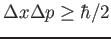
- 03-04-2016
Es
Dimostrare che la funzione d'onda dei momenti di un pacchetto gaussiano nelle coordinate e` ancora una gaussiana. Confrontare
le due larghezze.
Calcolare la funzione d'onda completa 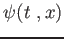 per un pacchetto Gaussiano a
per un pacchetto Gaussiano a  , e studiarne l'evoluzione.
, e studiarne l'evoluzione.
Calcolare: 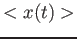 ,
, 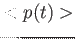 ,
, 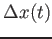 .
.
- 03-04-2016
Es
Determinare in quanto tempo un pacchetto gaussiano di larghezza 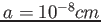 raddoppia la sua larghezza, ed in quanto tempo raggiunge
dimensioni macroscopiche, per:
raddoppia la sua larghezza, ed in quanto tempo raggiunge
dimensioni macroscopiche, per:
- un elettrone
- un palla da baseball di massa
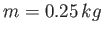 .
.
Studiare i casi limite:
-
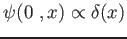 ;
;
-
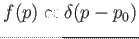
Calcolare la corrente per un' onda piana.
- 04-04-2016
Es
Risolvere l' equazione di Schrödinger per una particella in un potenziale a gradino.
A) Caso 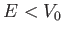 . Dimostrare che il coefficiente di riflessione
. Dimostrare che il coefficiente di riflessione 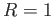 , e discutere il
significato della funzione d'onda sotto il gradino.
, e discutere il
significato della funzione d'onda sotto il gradino.
- 04-04-2016
Es
Risolvere l' equazione di Schrödinger per una particella in un potenziale a gradino.
B) Caso 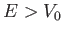 . Calcolare il coefficiente di riflessione
. Calcolare il coefficiente di riflessione 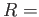 e di trasmissione
e di trasmissione 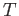 . Dimostrare
che
. Dimostrare
che 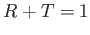
- 06-05-2016
Es
La buca di potenziale infinita: auto-funzioni e spettro dell'energia. Normalizzazione.
Funzioni d'onda dei momenti.
La buca di potenziale infinita simmetrica per riflessioni: ``parita''' degli stati.
- 06-05-2016
Es
La buca di potenziale semi-infinita:
Spettro all' interno della buca di potenziale finita.
- 10-05-2016
Es
Si consideri una barriera di potenziale rettangolare di base 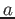 ed altezza
ed altezza 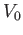 . Calcolare il coefficiente di tramissione
(``Effetto Tunnel'') quando
. Calcolare il coefficiente di tramissione
(``Effetto Tunnel'') quando 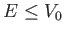 .
Ricavare la formula di Gamow per il coefficiente di trasmissione nel limite
.
Ricavare la formula di Gamow per il coefficiente di trasmissione nel limite
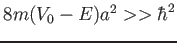
- 10-05-2016
Es
Usare la formula di Gamow per calcolare la probabilt` di decadimento-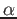 di un nucleo radiattivo.
Stimare la vita media di una particella
di un nucleo radiattivo.
Stimare la vita media di una particella 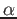 all'interno del nucleo.
all'interno del nucleo.
- 11-05-2016
Es
Calcolare il coefficiente di riflessione e trasmissione di una particella sopra una barriera di potenziale rettangolare
quando 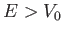 . Determinare quando
. Determinare quando 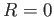 e
e 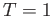 (``risonanza'').
(``risonanza'').
Risolvere l'equazione di Schrödinger per una particella in una ``scatola'' con pareti perfettamente riflettenti.
- 11-05-2016
Es
Stimare l'energia minima di un oscillatore armonico quantistico
usando il principio di Indeterminazione.
Risolvere l'equazione di Schrödinger per l'oscillatore armonico
in una dimensione. Andamenti asintotici della funzione d'onda.
Soluzione per serie col metodo di ricorrenza.
- 13-05-2016
Lo spettro dell' oscillatore armonico quantistico. I polinomi di Hermite.
- 12-05-2016
Es
Normalizzare la funzione d'onda dell'oscillatore armonico.
Confrontare la densità di probabilità del primo stato eccitato, i.e.
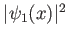 , con la probabilità classica.
, con la probabilità classica.
- 17-05-2016
Es
Calcolare lo spettro e le autofunzioni per una particella nel potenziale
| |
|
 |
|
| |
|
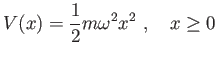 |
(9) |
Risolvere l'equazione di Schrödinger in un potenziale (oscillatore armonico anisotropo)
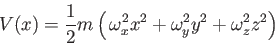 |
(10) |
Discutere la degerazione dei livelli nel limite isotropo.
- 17-05-2016
Quantizzazione dell' oscillatore armonico col metodo algebrico. L' algebra degli operatori di creazione/distruzione 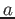 ,
, 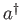 .
Definizione dello stato di ``vuoto'' e calcolo esplicito della funzione d'onda.
.
Definizione dello stato di ``vuoto'' e calcolo esplicito della funzione d'onda.
![\begin{displaymath}
I^{mn}= m a^2 \,\left(\,
\begin{array}[c]{lll}
2 & 1 & 0\\
1 & 2 & 0\\
0 & 0 & 4
\end{array}\,\right)
\end{displaymath}](img7.png)
![]() e dimensioni trasverse trascurabili,
determinare
e dimensioni trasverse trascurabili,
determinare ![]() ripetto il punto medio della sbarra.
ripetto il punto medio della sbarra.
![]() e
e ![]() .
.
![]()