Introduzione alla Fisica Teorica
A.A. 2014-15
Meccanica Analitica
- 03-03-2015:
Presentazione del corso:
obiettivi e contenuti. Testi di
riferimento e materiale bibliografico on-line.
Modalità di svolgimento dell'esame.
- 03-03-2015 :
La meccanica Newtoniana come teoria fenomenologica del moto a bassa velocità.
Il problema dei vincoli. Coordinate generalizzate.
- 04-03-2014 :
Gradi di libertà. Vincoli cinematici integrabili. Sistemi olonomi e sistemi
anolonomi. Spazio delle configurazioni. Velocità generalizzate: definizione
e relazione con le velocità nello spazio fisico. Energia cinetica
in termini delle velocità generalizzate.
- 05-03-2014:
Es. Si consideri un sistema di due particelle 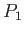 e
e 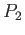 . La particella
. La particella 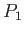 è
vincolata a muoversi lungo l'asse
è
vincolata a muoversi lungo l'asse 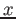 . La particella
. La particella 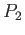 e collegata alla particella
e collegata alla particella 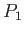 da una sbarra rigida di lunghezza
da una sbarra rigida di lunghezza 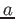 , di massa trascurabile.
, di massa trascurabile.
- Conteggiare il numero di gradi di libertà.
- Determinare un possibile sistema di coordinate generalizzate.
- Calcolare l'energia cinetica in funzione delle velocità generalizzate.
- 05-03-2014:
Es. Si consideri un cilindro che rotola, (senza strisciare), su un piano inclinato.
Dimostrare che il vincolo di rotolamento è integrabile e determinare il numero di gradi
di libertà.
Si consideri un disco di raggio 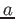 vincolato a rotalare, (senza strisciare), su un
piano orizzontale, mantenendosi in un piano verticale. Verificare che il vincolo non è integrabile.
vincolato a rotalare, (senza strisciare), su un
piano orizzontale, mantenendosi in un piano verticale. Verificare che il vincolo non è integrabile.
- 05-03-2015:
Forze conservative ed Energia cinetica generalizzate.
La `` funzione di Lagrange ''. Eq. di Eulero-Lagrange come generalizzazione delle equazioni di Newton.
Coordinate cicliche e costanti del moto.
- 10-03-2015:
Covarianza delle equazioni di Lagrange per trasformazioni generali di coordinate.
Moltiplicatori di Lagrange.
- 10-03-2014
Es.
Equazioni del moto di una particella libera in un sistema di coordinate rotante.
Pendolo come sistema `` vincolato ''.
Moto di una particella in caduta libera lungo una `` guida '' 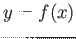 .
.
- 11-03-2015
Coordinate cicliche e costanti del moto. Potenziali centrali: conservazione del momento angolare e potenziale efficace.
Potenziali dipendenti dalle velocità.
L' energia nel formalismo Lagrangiano.
- 11-03-2015
Es.
Particella carica in un campo eletromagnetico esterno. Lagrangiana, equazioni del moto, energia totale del sistema.
Particella in caduta lungo una spira rotante. Lagrangiana equazioni, del moto, energia totale del sistema.
- 13-03-2015
Problema dei due-corpi in un campo di forze centrali. Separazione del moto del centro di massa
e del moto relativo. Simmetria sferica e conservazione del momento angolare. La II Legge di Keplero.
- 13-03-2015
Equazioni del moto. Potenziale efficace e classificazione delle possibili orbite.
Equazione dell' orbita.
- 17-03-2014
I Legge di Keplero: orbite ellittiche.
III Legge di Keplero: periodo di rivoluzione.
Correzioni al potenziale Newtoniano efficace e precessione del perielio di Mercurio.
- 17-03-2014
Es.
Determinare la distanza minima dall' origine su: i) un' orbita ellittica; ii) un' orbita parabolica; un' orbita iperbolica
Calcolare il periodo di rivoluzione di un satellite in ``orbita bassa'', circolare, a 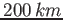 di altezza.
di altezza.
Calcolare il periodo di rivoluzione di un satellite in orbita ellittica, con perigeo a 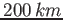 di altezza, ed apogeo a
di altezza, ed apogeo a
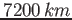 di altezza.
di altezza.
- 18-03-2015
Il calcolo delle variazioni. Funzionali e derivate funzionali. Principi di ``minimo'' secondo Fermat ed Hamilton.
- 18-03-2015
Es. Determinare il ``cammino piu` breve'' , nel piano, tra due punti dati, medianti il calcolo delle variazioni.
Verificare che la retta è effettivamente un ``minimo''.
- 20-03-2015
Es.
Ricavare la Legge di Snell dal Principio (variazionale) di Fermat.
Il problema della ``brachistocrona''.
- 20-03-2015
Equazioni di Lagrange, e traiettorie classiche, come estremali, dell' Integrale di Azione.
Variazione ad ``estremi fissi''.
- 24-03-2015
Es.
Calcolare l'azione per: i) una particella libera; ii) una particella in un campo di forze centrali; iii)
dimostrare che l'azione ricavata in ii) soddisfa l'equazione di Hamilton-Jacobi.
Dimostrare che l'invarianza per traslazioni spaziali implica la conservazione del momento lineare, e l'invarianza per
rotazioni la conservazione del momento angolare.
- 24-03-2015
Il Teorema di Emi Noether (versione semplificata). Le ``cariche di Noether''.
- 25-03-2015
Sistemi dinamici (cenni). Spazio delle fasi. Flusso di fase. Punti fissi.
- 25-03-2014
Es. Studiare i punti fissi e lo spazio di fase per:
i)un oscillatore armonico, uni-dimensionale;
ii)un oscillatore uni-dimensionale con costante elastica negativa;
- 27-3-2015
Lo spazio delle fasi ed i punti fissi, per il pendolo.
Discussione generale della relazione tra punti fissi e punti
di stazionarieta` del potenziale, per sistemi conservativi.
- 31-03-2015
L' ``Hamiltoniana'', definizione e significato fisico. Le quazioni di Hamilton.
La Trasformata di Legendre e la sua interpretazione geometrica.
- 31-03-2015
Es.
Data la Lagrangiana
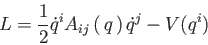 |
(1) |
Ricavare l' Hamiltoniana e le equazioni di Hamilton.
Data al Lagrangiana
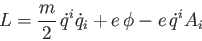 |
(2) |
ricavare:
i) l' Hamiltoninana;
ii) le equazioni di Hamilton.
Dimostrare che per un sistema autonomo l' Hamiltoniana è una costante del moto.
- 2-04-2014
Le equazioni di Hamilton da un principio variazionale.
L'equazione di Hamilton-Jacobi
- 2-04-2014
Equazione di Hamilton-Jacobi come limite classico dell'equazione di Schrödinger.
- 4-04-2014
Simmetria tra spazio e tempo in teorie relativistiche (cenni). Covariantizzazione
del formalismo Lagrangiano e a non-covarianza del formalismo Hamiltoniano.
- 4-04-2014
La ``forma simplettica'' (cenni). Le ``parentesi di Poisson'': definizione
e proprietà.
- 08-04-2015
Es. Ottenere le equazioni di Hamilton dalle parentesi di Poisson.
Calcolare le seguenti Parentesi di Poisson
- 08-04-2015
Trasformazioni canoniche infinitesime e funzione generatrice.
``Cariche di Noether'' come generatori di trasformazioni canoniche.
- 10-04-2015
Azione ed equazioni di Lagrange per una particella libera relativistica.
Coservazione dell'energia e del momento in meccanica relativistica.
- 10-04-2015
Difficoltà nel definire uan formulazione Hamiltoniana della particella
relativistica. Moltiplicatore di Lagrange ed azione equivalente on-shell.
Hamiltoniana come ``vincolo'' di mass-shell.
- 10-04-2015
La dinamica della particella relativistica nella ``gauge sincrona''. Azione in forma
Lagrangiana ed Hamiltoniana.
- 10-04-2015
L' elettromagnetismo come teoria Lagrangiana di un ``mezzo continuo''. Azione Lagrangiana
ed equazioni di Maxwell da un principio variazionale.
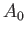 come moltiplicatore di Lagrange
e
come moltiplicatore di Lagrange
e
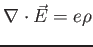 come ``vincolo''. Azione in forma Hamiltoniana.
come ``vincolo''. Azione in forma Hamiltoniana.
La crisi della fisica classica
- 15-04-2015
Il `` corpo nero ''. La Legge di Rayleigh-Jeans per la densità spettrale di energia
di corpo nero. La `` catastrofe ultravioletta ''.
- 15-04-2015
Es. Conteggiare i modi normali del campo elettromagnetico in una ``scatola'' con pareti conduttrici riflettenti.
Ricavare la legge di Rayleigh-Jeans utilizzando il teorema di equipartizione dell'energia.
- 17-04-2015
L' ipotesi di Planck: `` discretizzazione '' dell'energia della radiazione di corpo-nero.
- 17-04-2015
Es.
Calcolare la Funzione di Partizione di Planck:
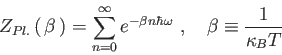 |
(4) |
Nota 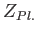 ricavare la densità spettrale di energia a temperatura
ricavare la densità spettrale di energia a temperatura 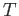 .
.
- 17-04-2015
L' effetto Foto-elettrico. La spiegazione di Einstein e la natura corpuscolare della luce.
Il `` fotone '' come `` quanto '' di energia elettromagnetica.
- 21-04-2015
La natura ondulatoria vs la natura corpuscolare delle luce. L'esperimento di diffrazione di
Young come ``diffusione'' di fotoni.
- 21-04-2015
Diffusione di raggi-x da elettroni. Il picco primario e secondario.
L' effetto Compton come urto-elastico fotone-elettrone.
- 22-04-2015
Interpretazione fisica dei picchi principale e secondario, nell' effetto Compton. Scattering di
Rayleigh e Scattering Compton.
- 22-04-2015
Il `` microscopio '' di Bhor ed il Principio
di Indeterminazione di Heisemberg.
- 24-04-2015
Gli spettri degli atomi idrogenoidi. La costante di
Rydberg e la formula di Balmer.
- 24-04-2015
I postulati di Bohr. La quantizzazione del momento angolare. Spettro degli atomi idrogenoidi.
L'ipotesi di De Broglie. Velocità di fase e velocità di gruppo.
- 28-04-2015
Ricavare la quantizzazione dell'energia e del momento
angolare dalla condizione di quantizzazione di Bohr-Sommerfeld
- 28-04-2015
Descrizione qualitative del esperimento di Davidson-Germer: diffrazione di elettroni da una doppia fenditura.
Comportamento corpuscolare vs comportamento ondulatorio
- 29-04-2015
- 29-04-2015
Descrizione quantitativa dell' esperimento di Davidson-Germer. Interpretazione probabilistica della funzione
d'onda.
Meccanica Ondulatoria
- 05-05-2015
Onde piane come autofunzioni del momento e dell'energia.
L' equazione di Schrodinger.
- 05-05-2015
L' equazione di Schrodinger stazionaria: soluzione col metodo di separazione delle variabili.
Equazione di continuità per una particella in moto lungo l'asse-x.
- 06-05-2015
Equazione di continuità in tre dimensioni. Forma esplicita per autofunzioni del momento.
Onda piana come pacchetto ``lungo'' per una singola particella, o come descrizione effettiva
di un fascio di particelle di momento definito.
- 06-05-2015
Funzione d' onda in forma ``polare'' . Equazioni per il modulo e la fase. Equazione di
Hamilton-Jacobi `` quantistica'' e funzioni d' onda '' semi-classiche ``.
Funzioni d'onda nello spazio dei momenti.
- 08-05-2015
Es. Dimostrare che un pacchetto d'onde Gaussiano in momento è anche Gaussiano in posizione.
Dimostrare che un pacchetto Gaussiano corrisponde ad uno stato di minima indeterminazione per una
particella libera.
- 08-05-2015
Es. Dimostrare che nel corso della sua evoluzione il pacchetto resta Gaussiano, ma che il
picco della distribuzione di probabilità si sposta e la larghezza cresce monotonamente.
Dimostrare che i valori medi 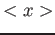 ,
, 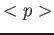 soddisfano le equazioni del moto classiche, di una
particella libera.
soddisfano le equazioni del moto classiche, di una
particella libera.
Calcolare quanto tempo impiega un pacchetto gaussiano con 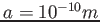 , e
, e
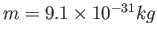 , per:
, per:
i) raddoppiare la sua estensione lineare, i.e. calcolare 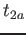 :
: 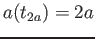 ;
ii) estendersi fino ad una distanza macroscopica
;
ii) estendersi fino ad una distanza macroscopica 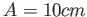 ;
iii) ripetere i conti i) e ii) per una massa
;
iii) ripetere i conti i) e ii) per una massa 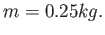
- 12-05-2015
- 12-05-2014
Es. Si consideri un particella nel potenziale a gradino
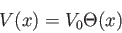 |
(5) |
1) Discutere le condizioni di continuità di 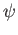 e
e 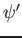 in
in  .
.
2) Risolvere l'equazione d' onda nel caso 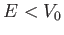 .
.
3) Determinare le ampiezze dell'onda incidente e di quella riflessa in funzione dell'ampiezza dell'onda
trasmessa.
4) Calcolare il coefficiente di riflession 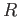 della barriera, la `` lunghezza di penetrazione '' e discuterne
la misurabilità.
della barriera, la `` lunghezza di penetrazione '' e discuterne
la misurabilità.
- 13-05-2015
- 13-05-2014
Es. Si consideri un particella nel potenziale a gradino
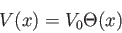 |
(6) |
Risolvere l'equazione d'onda per 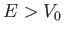 . Determinare il coefficiente di riflessione
. Determinare il coefficiente di riflessione 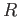 e trasmissione
e trasmissione 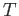 . Verificare
che
. Verificare
che 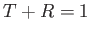 .
.
Si consideri una barriera di potenziale rettangolare di base 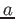 ed altezza
ed altezza 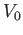 . Calcolare il coefficiente di tramissione
(``Effetto Tunnel''). Formula di Gamow e decadimento
. Calcolare il coefficiente di tramissione
(``Effetto Tunnel''). Formula di Gamow e decadimento 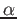 dell' Uranio
dell' Uranio  .
.
- 15-05-2015
- 15-05-2015
Es.
Si consideri la buca di potenziale ``infinita``
| |
|
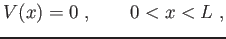 |
(7) |
| |
|
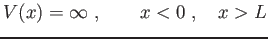 |
(8) |
i) Discutere le condizioni di ''saldatura'' in 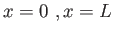 .
.
ii) Risolvere l'equazione d'onda e determinare lo spettro dell'energia.
iii) Normalizzare la funzione d'onda.
iv) Ricavare l'energia dello stato fondamentale dal Prinicipio di Indeterminazione.
v) Traslare
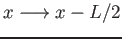 . Discutere le proprieta` di simmetria delle
auto-funzioni per riflessioni
. Discutere le proprieta` di simmetria delle
auto-funzioni per riflessioni
 .
.
Si consideri la buca di potenziale ``finita``
| |
|
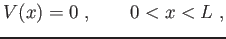 |
(9) |
| |
|
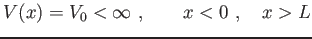 |
(10) |
Discutere il tipo di soluzioni e lo spettro dell' energia, per 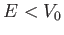 .
.
- 19-05-2015
- 19-05-2015
Es.
Si consideri la buca di potenziale ``finita``
| |
|
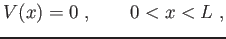 |
(11) |
| |
|
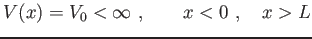 |
(12) |
Discutere il tipo di soluzioni e lo spettro dell' energia, per 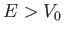 .
Si ricavi il coefficiente di trasmissione e si determini quando
.
Si ricavi il coefficiente di trasmissione e si determini quando 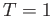 .
.
Determinare l'energia minima di un oscillatore armonico quantistico
usando il principio di Indeterminazione.
- 20-05-2015
Es.
L'equazione di Schrodinger per l'oscillatore armonico
in una dimensione. Andamenti asintotici della funzione d'onda.
Soluzione col metodo di ricorrenza ed auto-valori dell'energia.
Euro Spallucci
2015-05-26
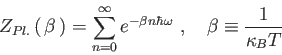
![]() ricavare la densità spettrale di energia a temperatura
ricavare la densità spettrale di energia a temperatura ![]() .
.