Introduzione alla Fisica Teorica
A.A. 2013-14
Meccanica Analitica
- 04-03-2014:
Presentazione del corso:
motivazioni ed obiettivi; contenuti. Testi di
riferimento e materiale bibliografico on-line.
- 04-03-2014 :
La `` mappa '' della Fisica Teorica. L' idea di
`` Unificazione '' come tema di fondo della
Fisica Teorica.
- 05-03-2014 :
Coordinate generalizzate. Gradi di libertà
e vincoli. Velocità generalizzate.
Forze generalizzate.
- 05-03-2014:
Es. Gradi di libertà di una particella:
i) su una retta
ii) nel piano
iii) nello spazio.
Gradi di libertà di un corpo rigido:
i) nel piano
ii)nello spazio.
Gradi di libertà del pendolo matematico.
- 07-03-2014:
Forze conservative ed Energia cinetica generalizzate.
La `` funzione di Lagrange ''. Eq. di Eulero-Lagrange come generalizzazione delle equazioni di Newton.
Coordinate cicliche e costanti del moto.
- 07-03-2014:
Es. Particlla sul piano in presenza di forze centrali:
ricavare la Lagrangiana;
scrivere le equazioni di Lagrange;
consevazione del momento angolare;
potenziale efficace.
- 11-03-2014
Es. Equazioni del moto di una particella libera in un sistema di coordinate rotante.
- 11-03-2014
Es. Pendolo come sistema `` vincolato ''. Moltiplicatori di Lagrange.
Moto di una particella in caduta liber lungo una `` guida '' 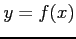 . Moltiplicatore di Lagrange come
`` costante di accoppiamento '' particella-potenziale vincolare.
. Moltiplicatore di Lagrange come
`` costante di accoppiamento '' particella-potenziale vincolare.
- 12-03-2014
Es.
Equazioni del moto di una particella in caduta lungo un piano inclinato mobile.
Oscillatori accoppiati: calcolo dei modi normali di vibrazione.
- 12-03-2014
``Energia'' conservata nel formalismo lagrangiano.
Lagrangiana per una particella carica in un campo elettro-magnetico esterno.
- 14-03-2014
Energia conservata per una particella carica in un campo elettro-magnetico esterno.
- 14-03-2014
Soluzione dell'equazioni del moto col metodo di separazione delle variabili.
Spazio di fase. Flusso di fase. Punti fissi
- 18-03-2014
Es. Studiare i punti fissi e lo spazio di fase per:
i) oscillatore armonico, uni-dimensionale;
ii)`` oscillatore invertito'', uni-dimensionale;
iii) pendolo matematico
- 18-03-2014
Punti fissi ellittici, iperbolici, marginali.
Metodo generale per determinare i punti fissi e lo spazio di fase
di un sistema meccanico ad 1 grado di libertà.
- 19-03-2014
Problema dei due-corpi in un campo di forze centrali. Separazione del moto del centro di massa
e del moto relativo. Simmetria sferica e conservazione del momento angolare. La II Legge di Keplero.
- 19-03-2014
Equazioni del moto. Potenziale efficace e classificazione delle possibili orbite.
Condizioni di esistenza per l'orbita circolare stabile.
- 21-03-2014
I Legge di Keplero: orbite.
III Legge di Keplero: periodo di rivoluzione.
Correzzioni al potenziale newtoniano e precessione del perielio di Mercurio.
- 21-03-2014
Es.
Studiare i punti fissi (eventuali) del potenziale efficace newtoniano, e disegnare lo spazio
di fase.
Calclare il periodo di rivoluzione di un satellite in ``orbita bassa'', circolare, a 200 km di altezza.
Calclare il periodo di rivoluzione di un satellite in orbita ellittica, con perigeo a 200 km di altezza, ed apogeo a 7200 km di altezza.
- 25-03-2014
Il problema del ``cammino piu` breve''. Equazioni di Eulero-Lagrange. Derivate funzionali e calcolo
delle variazioni. L' integrale di Azione.
- 25-03-2014
Equazioni di Lagrange, e traiettorie classiche, come estremali, dell' Integrale di Azione.
Variazione ad ``estremi fissi''.
- 26-03-2014
Es.
Calcolare l'azione per una particella libera.
Determinare la forma della funzione 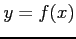 che genera la superficie di rivoluzione di area minima.
che genera la superficie di rivoluzione di area minima.
Determinare la forma della ``brachistocrona'' in un campo gravitazionale costante.
- 26-03-2014
Variazione seconda dell' azione di un oscillatore armonico, attorno alla soluzione classica.
Condizioni di minimo, massimo e flesso ( punto a sella ).
- 27-03-2014
Es.
Invarianza per traslazioni spaziali e conservazione del momento.
Invarianza per rotazioni e conservazione del momento angolare.
Invarianza per traslazioni temporali e conservazione dell' energia.
- 27-03-2014
Il Teorema di Emi Noether. ``Cariche'' conservate.
Invarianza di gauge, equazione di continuità e conservazione della carica elettrica.
- 1-04-2014
L' ``Hamiltoniana''. Le quazioni di Hamilton.
La Trasformata di Legendre.
- 1-04-2014
Es.
Data al Lagrangiana
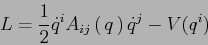 |
(1) |
Ricavare l' Hamiltoniana e le equazioni di Hamilton.
Data al Lagrangiana
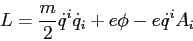 |
(2) |
ricavare:
i) l' Hamiltoninana;
ii) le equazioni di Hamilton;
iii) l'equzione del moto in forma Lagrangiana
- 2-04-2014
Le equazioni di Hamilton da un principio variazionale.
L'equazione di Hamilton-Jacobi
- 2-04-2014
Approssimazione iconale dell'ottica geometrica ed equazione di Hamilton-Jacobi.
Equazione di Hamilton-Jacobi come limite classico dell'equazione di Schrödinger.
- 4-04-2014
La non-covarianza del formalismo Hamiltoniano.
Le ``parentesi di Poisson''. Parentesi di Poisson
e ``commutatori''.
- 4-04-2014
Es. Ottenere le equazioni di Hamilton dalle parentesi di Poisson.
Calcolare le seguenti parentesi di Poisson:
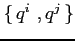 ,
,
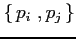 ,
,
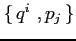 .
.
La crisi della fisica classica
- 8-04-2014
La radiazione di `` corpo nero ''. La Legge di Rayleigh-Jeans e la `` catastrofe ultravioletta ''.
L' ipotesi di Planck: `` quantizzazione '' come `` discretizzazione '' di una variable
classicamente continua. La densità spettrale di energia, di Planck, e la legge di Stefan-Boltzmann.
- 8-04-2014
Es. Calcolare i modi normali del campo elettromagnetico in una ``scatola'' con pareti riflettenti.
Calcolare la Funzione di Partizione di Planck:
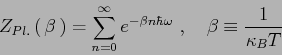 |
(3) |
Nota 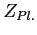 ricavare la densità spettrale di energia a temperatura
ricavare la densità spettrale di energia a temperatura 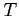 .
.
Calcolare l'energia elettromagnetica totale nella scatola.
- 9-04-2014
L' effetto Foto-elettrico. La spiegazione di Einstein e la natura corpuscolare della luce.
Il `` fotone '' come `` quanto '' di energia elettromagnetica.
- 9-04-2014
L' effetto Compton come urto-elastico fotone-elettrone. Il `` microscopio '' di Heisenberg.
- 11-04-2014
L' atomo di Bhor. Quantizzazione del momento angolare. Orbite discrete ed spettro dei
livelli energetici. Formula di Rydberg.
- 11-04-2014
L' ipotesi di DeBrogliè. L' equazione d'onda di Schrödinger.
- 15-04-2014
L' esperimento di Davidson e Germer: diffrazione di elettroni da una doppia fenditura.
Intensita` dell' onda di De Broglie e intensita` di un fascio di particelle.
Interpretazione di Born della funzione d'onda.
- 15-04-2014
``Anatomia'' dell'esperimento di diffrazione. Il dualismo onda/particella.
Impossibilita` di definire una traiettoria classica.
- 16-04-2014
Es.
Costruire un rappresentazione "vettoriale" del moto uni-dimensionale di una particella. Moto nello spazio fisico vs. moto
sulla sfera unitaria nello spazio vettoriale. Interpretazione fisica "alla Born" dei vettori di stato.
Introduzione alla Meccanica Meccanica Quantistica
- 16-04-2014
La notazione di Dirac: i "bra" ed i "ket". Funzioni a quadrato sommabile come vettori complessi
ad infinite componenti. Lo Spazio di Hilbert e la sua importanza per la meccanica quantistica. Operatori
ed "elementi di matrice".
- 23-04-2014
Valori di aspettazione e valori medi. Scarto quadratico medio come ``incertezza''.
Operatore momento
- 23-04-2014
Operatori Hemitiani. Operatore Hamiltoniano. Teorema di Ehrnfest.
- 29-04-2014
Es. Calcolare :
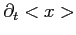 e
e
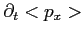 utilizzando l' eq. di Schrödinger.
utilizzando l' eq. di Schrödinger.
Dimostrare che l' eq. di Schrödinger per potenziali independenti dal tempo si può risolvere col metodo di separazione
delle variabili.
- 29-04-2014
Es.
Corrente di probabilità e leggi di conservazione locale e globale.
L' eq. di Schrödinger stazionaria come equazione agli auto-valori per l' Hamiltoniano.
- 30-04-2014
Es.
Risolvere l'eq. di Schrödinger stazionaria per una particella libera in 1D.
Trovare la soluzione generale col metodo di Fourier. Determinare la condizione di normalizzazione della funzione
d'onda nello spazio dei momenti.
- 30-04-2014
Es.
Sia lo stato iniziale di una particella descritto dal pacchetto d'onda gaussiano
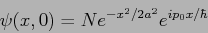 |
(4) |
i) determinare il coeeficiente di normalizzazione 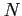 ; ii) il valor medio
; ii) il valor medio 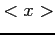 ; iii) il valor medio
; iii) il valor medio 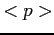 , iv) l'incertezza
, iv) l'incertezza 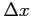 ;
v) la funzione d'onda nello spazio dei momenti:
;
v) la funzione d'onda nello spazio dei momenti:
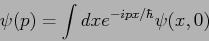 |
(5) |
Determinare l'evoluzione del pachetto, i.e. calcolare
![\begin{displaymath}
\psi(x, t)= \int \frac{dp}{2\pi\hbar} \exp\left[\, i\left(\, px - \frac{p^2}{2m}t\,\right)\,\right]\psi(p)
\end{displaymath}](img18.png) |
(6) |
- 06-05-2014
Es.
Data 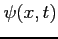 determinare l'evoluzione dei valori medi
determinare l'evoluzione dei valori medi 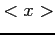 ,
, 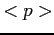 , e delle
incertezze
, e delle
incertezze 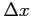 ,
, 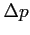 .
.
Calcolare quanto tempo impiega un pacchetto gaussiano con 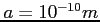 , e
, e
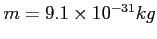 , per:
, per:
i) raddoppiare la sua estensione lineare, i.e. calcolare 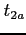 :
: 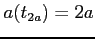 ;
ii estendersi fino ad una distanza macroscopica
;
ii estendersi fino ad una distanza macroscopica 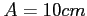 ;
iii) ripetere i conti i) e ii) per una massa
;
iii) ripetere i conti i) e ii) per una massa 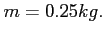
- 06-05-2014
Il Principio di Heisenberg ( per il pacchetto gaussiano ).
Velocità di fase e velocità di gruppo per la sovrapposizione di due onde piane.
- 07-05-2014
Velocità di fase e velocità di gruppo per un generico pacchetto d'onda.
Principio di Indeterminazione e stabilit`a dell'atomo di idrogeno.
- 07-05-2014
Es. Calcolare gli autovalori e le autofunzioni di una particella in una buca
di potenziale, rettangolare, infinita.
- 13-05-2014
Es. Calcolare i seguenti valori medi per una particella nella buca
di potenziale, rettangolare, infinita: 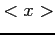 ,
, 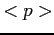 ,
, 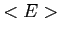 .
.
Dimostrare che l'energia cinetica della particella nella buca deriva unicamente dal principio
di indeterminazione.
- 13-05-2014
Autostati dell' Hamiltoniano come valori misurabili dell'energia.
Significato fisico dei coefficienti dello sviluppo in autostati dell'energia.
- 14-05-2014
Es. Calcolare il coefficiente di riflessione di una ``barriera infinita'' nell'origine.
Si consideri un potenziale a ``gradino'' di altezza finita 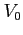 per
per 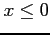 . Risolvere l'equazione di Schrodinger per
. Risolvere l'equazione di Schrodinger per 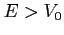 ed
imporre le condizioni di continuià sulla funzione d'onda e la sua derivata prima.
ed
imporre le condizioni di continuià sulla funzione d'onda e la sua derivata prima.
- 14-05-2014
Es.
Calcolare il coefficiente di riflessione e di trasmissione del ``gradino''. Studiare i limiti 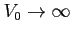 e
e 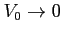 .
.
- 15-05-2014
Es. Calcolare il coefficiente di riflessione e di trasmissione del ``gradino'' per 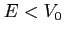 .
Determinare la forma della funzione d'onda sotto il gradino. Calcolare lo ``sfasamento'' tra l'onda incidente e l'onda
riflessa.
.
Determinare la forma della funzione d'onda sotto il gradino. Calcolare lo ``sfasamento'' tra l'onda incidente e l'onda
riflessa.
- 15-05-2014
Es.
Calcolare il coefficiente di trasmissione attraverso una barriera di potenziale rettangolare
(Effetto Tunnel)
- 16-05-2014
Es. Calcolare il coefficente di trasmissione e di riflessione
di una buca di potenziale rettangolare. Determinare le
condizioni di "trasparenza" totale della buca (Effetto Ramsauer).
- 16-05-2014
Es. Risolvere l'equazione di Schrodinger all' interno della
buca. Studiare lo spettro dei livelli energetici.
Parita` degli stati legati nella buca.
- 21-05-2014
L'equazione di Schrodinger per l'oscillatore armonico
in una dimensione. Soluzione col metodo di ricorrenza.
- 21-05-2014
Spettro dei livelli energetici e possibili interpretazioni fisiche.
Energia di punto-zero come conseguenza del principio di indeterminazione.
- 23-05-2014
I polinomi di Hermite e le funzioni d'onda dell' oscillatore armonico.
L'algebra degli operatori 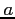 ,
, 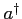 definizione e proprietà.
definizione e proprietà.
- 23-05-2014
L' Hamiltoniano in termini di 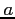 ,
, 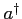 . Lo stato
fondamentale come stato di ``vuoto''.
. Lo stato
fondamentale come stato di ``vuoto''.
- 27-05-2014
Es.
Ricavare le funzioni d'onda dell' oscillatore armonico partendo da 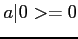 .
Calcolare i valori medi di
.
Calcolare i valori medi di
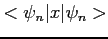 ,
,
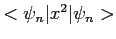 ,
,
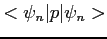 ,
,
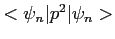 . Dimostrare che
. Dimostrare che
 |
(7) |
- 27-05-2014
Domande e risposte sugli argomenti svolti nel corso.
Euro Spallucci
2014-05-29
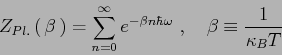
![]() ricavare la densità spettrale di energia a temperatura
ricavare la densità spettrale di energia a temperatura ![]() .
.
![\begin{displaymath}
\psi(x, t)= \int \frac{dp}{2\pi\hbar} \exp\left[\, i\left(\, px - \frac{p^2}{2m}t\,\right)\,\right]\psi(p)
\end{displaymath}](img18.png)