Relatività B
A.A. 2001-02

Equazioni di Campo.

1. 22-04-02:
   Presentazione del corso e collegamenti con il modulo A. Richiami sulle equazioni di campo di Einstein.
2. 22-04-02:
   Eserc. Dimostrare che le equazioni di Einstein, nel vuoto, si possono ricavare da un principio variazionale (Azione di Hilbert-Einstein).
3. 24-04-02:
   Eserc. Mostrare che la definizione covariante generale del tensore energia-impulso, 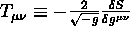, implica 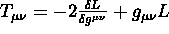dove ;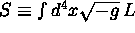
   calcolare il 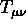per il campo elettromagnetico libero, e verificare che in un sistema di coordinate localmente inerziali
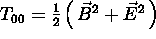
4. 24-04-02:
   Trasformazioni di Coordinate Attive e Passive. Variazione Totale e Variazione Locale di campi tensoriali per i due tipi di trasformazioni.
5. 26-04-02:
   Eserc. Calcolare la Variazione Locale, per 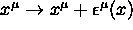di:
   i) un campo scalare;
   ii) del tensore metrico;
   iii) dimostrare che la variazione locale del tensore metrico può essere scritta come .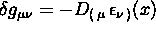
   Eserc. Dimostrare che l' invarianza della' azione di materia per 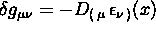implica ( a meno di termini di superficie ) che .
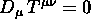6. 26-04-02 :
   Vettori di Killing e Leggi di Conservazione in Relatività Generale. Vettore di Killing Tipo-Tempo e conservazione del quadri-momento. Significato geometrico dei Vettori di Killing: Isometrie.
   Invarianza di Scala Locale e condizione di traccia nulla del tensore energia-impulso.
7. 29-04-02 :
   Eserc. Calcolare il tensore energia-impulso del campo eletromagnetico in D dimensioni;
   verificare che la sua traccia è nulla per D=4;
   Eserc. Calcolare il tensore energia-impulso di un campo scalare massivo in D dimensioni;
   verificare che la sua traccia è nulla per D=2 e massa zero.
   
8. 29-04-02 :
   Anomalie di Gauge, Anomalie Gravitazionali, Anomalie di Traccia, in teorie di campo e teorie di stringa ( CENNI ).
9. 02-05-02 :
   Le equazioni di Einstein in presenza di sorgenti. Principo variazionale di Hilbert-Einstein in presenza di materia.
   

Le soluzioni di: Schwartzschild, Reissner-Nordström, Kerr(-Newman)

1. 02-05-02 :
   Equazioni di Einstein nel vuoto, con costante cosmologica nulla.
   Forma generale del 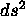per una geometria a simmetria sferica, ed equazioni per i coefficienti metrici.
2. 03-05-02 :
   Soluzione di Schwartzschild. Limite di campo debole dell metrica di Schwartzschild e significato fisico del ``raggio gravitazionale''.
   Teorema di Birkoff ( CENNI ).
3. 03-05-02 :
   Equazione delle Geodetiche nella metrica di Schwartzschild. Costanti del moto.
4. 06-05-02 :
   Potenziale Efficace per la metrica di Schwartzschild. Equazione delle orbite. Red-shift gravitazionale.
5. 06-05-02 :
   Eserc. Calcolare l'angolo di Precessione dell' orbita di Mercurio.
   Eserc. Stimare col Principio di Equivalenza l' angolo di deflessione della luce vicino al sole.
6. 07-05-02 :
   Eserc. Calcolare esattamente l'angolo di deflessione di un raggio di luce che passa vicino alla superficie del Sole.
   Eserc. Calcolare le forze di marea in .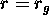
7. 07-05-02 :
   La metrica di Schartzschild per . Singolarità di curvatura e singolarità di coordinate. Struttura dei coni-luce in coordinate polari standard. La superficie 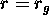come Orizzonte di Eventi.
8. 08-05-02 :
   Coordinate di cono-luce.
   La metrica di Schwartzschild in coordinate di Eddington-Finkelstein. Struttura dei coni-luce.
9. 08-05-02 :
   Le coordinate di Kruskal-Szekeres e la massima estensione analitica della metrica di Schartzschild.
10. 13-05-02 :
    Il Diagramma di Kruskal. Buchi Neri e Buchi Bianchi. Orizzonti di eventi futuri e passati.
11. 13-05-02 :
    Diagrammi di Embedding per sezioni U=cost. della metrica di Schwartzschild in coordinate di Kruskal. Il ``Ponte di Einstein-Rosen'' come esempio di ``wormhole non-attraversabile''.
12. 15-05-02 :
    Il Diagramma di Kruskal per la metrica di una stella:
    i) caso stazionario, ;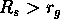
    ii) caso di un collasso gravitazionale, .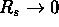
13. 15-05-02 :
    Instabilita` classica di un buco bianco.
    Evaporazione quantistica di un buco nero primordiale; Temperatura di Hawking ed entropia di un buco nero; il problema dell' ``Informazione'' ( CENNI ).
14. 16-05-02 :
    Stadi finali del collasso gravitazionale di una stella. Aspetti fenomenologici di Nane Bianche e Stelle di Neutroni.
15. 16-05-02 :
    Stelle di Neutroni e Supernovae.
    Stelle di neutroni e PULSARs.
    Buchi neri in sistemi binari:Cigno X-1.
16. 20-05-02 :
    Eserc. Calcolare la densità di particelle per un gas degenere di fermioni.
    Eserc. Calcolare la densità di energia media per un gas degenere di fermioni.
    Eserc. Calcolare l' energia di autointerazione gravitazionale per un gas degenere di fermioni.
17. 20-05-02 :
    Eserc. Studiare un modello di nana-bianca non-relativistica come sfera omogenea di fermioni degeneri, auto-gravitanti. Si assuma che la massa della stella è dominata dalla componente ``pesante'', del gas i.e. protoni e neutroni, mentre la pressione di degenarazione è determinata dalla componente leggera del gas, i.e. elettroni. Determinare la relazione tra massa e raggio della stella, e stimare il raggio di un nana-bianca di una massa solare.
    
18. 22-05-02 :
    Eserc. Calcolare la pressione di degenerazione per un gas di fermioni: i) non-relativistic; ii) relativistici
    Eserc. Determinare la densità critica di fermioni corrispondente a .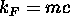
    Eserc. Stimare la massa limite (Massa di Chandrasekar) per una nana-bianca relativistica; utilizzare questo risultato per calcolare il corrispondente valore limite, i.e. limite di Oppenheimer-Volkoff, per una stella di neutroni.
    
19. 22-05-02 :
    La soluzione di Reissner-Nordström delle equazioni di Einstein. Caso .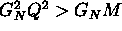
    La ``Singolarità Nuda.''
20. 23-05-02 :
    Il ``Principio di Censura Cosmica''.
    ``Neutralizzazione della carica elettrica, per creazione di coppie 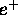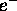, nel collasso di un oggetto con 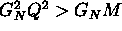, e formazione di un buco nero neutro invece di una ``singolarità nuda'' ( CENNI ).
21. 23-05-02 :
    La soluzione di Reissner-Nordström delle equazioni di Einstein. Caso 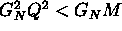: il buco-nero elettricamente carico. Rappresentazione grafica della massima estensione analitica della metrica. Il ``wormhole attraversabile'' di Reissner-Nordström.
22. 27-05-02 :
    Scaricamento di un buco nero per produzione di coppie 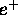, 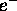; ``Transizione tra un Buco Nero di Reissner-Nordström ed uno di Schwartzschild'': ( CENNI ).
    Il buco nero `` estremale'' con .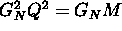
23. 27-05-02 :
    La metrica di Kerr in coordinate di Boyer-Lindquist.
    La singolarità anulare di curvatura.
24. 29-05-02 :
    Continuazione analitica della metrica di Kerr ad r<0 ( CENNI ). Anti-gravità in r<0 e curve time-like chiuse ( ``La Macchina del Tempo'' ) attorno alla singolarità anulare.
    
25. 29-05-02 :
    Eserc. Determinare la posizione degli orizzonti di eventi e della superficie di red-shift infinito della metrica di Kerr.
    Eserc. Studiare i coni-luce nel piano equatoriale 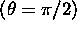della metrica di Kerr;
    calcolare la velocità angolare di un fotone sulla superficie di red-shift infinito e sull'orizzonte di eventi.
26. 30-05-02 :
    Estrazione di energia da un buco nero di Kerr: il ``processo di Penrose''.
    La massa irriducibile di un buco nero.
27. 30-05-02 :
    Eserc. Calcolare la velocità angolare di un fotone sulla superficie di infinito red-shift e sull' orizzonte d'eventi di un buconero di Kerr.
    Eserc. Calcolare come varia la massa irriducibile di un buco nero in funzione delle variazioni 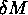e .
    
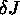28. 03-06-02 :
    Eserc. Calcolare la superficie dell'orizzonte di eventi di un buconero di Kerr; determinare la relazione tra area dell' orizzonte e massa irriducibile.
    Le Leggi della ``Termodinamica dei Buchineri'' ( CENNI )

I modelli di Friedmann per l' Universo a grande scala.

1. 03-06-02 :
   Aspetti fenomenologici nell' universo a grande scala. Red-shift Cosmologico. Legge di Hubble. Radiazione cosmica di fondo.
2. 05-06-02 :
   Introduzione al Modello Cosmologico Standard. Omogenità ed isotropia della distribuzione di materia e della radiazione di fondo.
3. 05-06-02 :
   Omogeneità, Isotropia e geometria di una tre-superficie. La metrica di Robertson-Walker.
   Eserc. Mostrare che 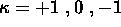descrivono, rispettivamente, una tre-sfera, un tre-piano, un tre-iperboloide.
4. 06-06-02 :
   Eserc. Data la metrica di Robertson-Walker calcolare:
   i) i simboli di Christoffel;
   ii) le componenti del tensore di Ricci.
5. 06-06-02 :
   Eserc. Ricavare la Legge di Hubble, ed il red-shift di un fotone dall' elemento di linea di Robertson-Walker.
   Eserc. Si consideri il 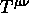di un fluido perfetto nella metrica di Robertson-Walker, in coordinate in cui 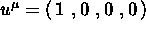. Scrivere la forma esplicita di 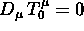; data l' equazione di stato 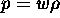si integri la precedente equazione per trovare come 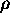dipende dal fattore di scala R(t).
6. 10-06-02 :
   Eserc. Mostrare che il 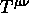di una radiazione, o di un sistema di particelle relativitiche, descritto come un fluido perfetto, corrisponde a w=1/3.
   Eserc. Si considerino i tre casi: 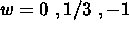. Determinare la dipendenza di 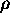dal fattore di scala R(t) nei tre casi.
7. 10-06-02 :
   La Densità Critica.
   Il problema della Materia Oscura. MACHOs e WIMPs.
   Eserc. Determinare la forma esplicita di R(t) in un modello con p=0 e .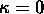
8. 12-06-02 :
   Eserc. Determinare la forma esplicita di R(t) in un modello con p=0 e 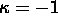; mostrare che per 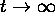la soluzione tende allo spaziotempo piatto.
   Eserc. Determinare la forma esplicita di R(t) in un modello con p=0 e .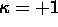
9. 12-06-02 :
   Eserc. Determinare la forma esplicita di R(t) in un modello con 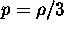e .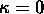
   Eserc. Determinare la forma esplicita di R(t) in un modello con 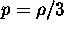e .
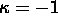10. 13-06-02 :
    Eserc. Studiare l'andamento asintotico per 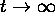di R(t) e 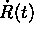per i modelli di Friedman aperti (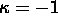) con:
    i) p=0;
    ii) .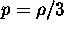
    Eserc. Risolvere l' equazione per R(t) per un modello di Friedmann ``dominato dal vuoto'' nei casi:
    i) , ;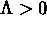
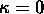    ii) , ;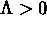
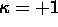    iii) , .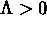
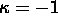11. 13-06-02 :
    Eserc. Determinare la relazione tra età e temperatura dell' universo, in un modello di Friedmann con 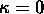, e dominato da una radiazione di corpo-nero a temperatura T.
    Eserc. Determinare la densitaà di energia di un gas di bosoni relativistici, i.e. 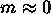, ad alta temperatura, usando la distribuzione di Bose-Einstein.
    Eserc. Determinare la densitaà di energia di un gas di fermioni relativistici, i.e. 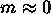, ad alta temperatura, usando la distribuzione di Fermi-Dirac.
    Il problema della asimmetria materia-antimateria nell'universo primordiale: ( CENNI ).

 
• About this document ...