


Next: About this document
Corso: Relatività A
A.A. 2001-02
Relatività Speciale e Gravitazione
- 02-10-02: Presentazione del corso. Contenuti e motivazioni.
Ruolo attuale
della Relatività Generale nella Fisica Teorica delle Alte Energie.
- 02-10-02: Notazione e convenzioni. Coordinate. Trasformazioni
di Lorentz come esempio di trasformazioni di coordinate. Covarianza
delle leggi fisiche per trasformazioni di coordinate. Elemento di
linea di Minkowski. Segnatura.
- 03-10-02: Covarianza ed Invarianza di Lorentz. Tempo proprio.
4-velocità e 4-momento.
- 03-10-02:
Eserc. Mostrare che 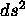 è un
invariante di Lorentz.
Calcolare il modulo della 4-velocità. Calcolare il modulo del
4-momento.
è un
invariante di Lorentz.
Calcolare il modulo della 4-velocità. Calcolare il modulo del
4-momento.
- 04-10-02:
Eserc. Derivazione euristica delle
equazioni d'onda per il campo elettromagnetico.
- 04-10-02: Gravità newtoniana vs Relatività Ristretta.
Il problema della sorgente. Massa Inerziale,
Massa Gravitazionale Attiva, Massa Gravitazionale Passiva. Principio
di Equivalenza (Debole).
- 09-10-02: Esperimento concettuale per provare che la sorgente
del campo garivtazionale deve essere la mass-energy, e non la massa
di riposo. Non-linearit`a di una teoria relativistica della
gravitazione.
- 09-10-02:
Eserc. determinare i ``coefficienti
metrici'' nei seguenti casi:
i) piano euclideo in coordinate cartesiane e coordinate polari;
ii) spazio euclideo tri-dimensionale in coordinate cartesiane e
coordinate polari;
iii) spazio-tempo di Minkowski in coordinate cartesiane e coordinate
polari.
- 10-10-02: ``Coordinate Piatte'' e ``Coordinate Curvilinee''.
Eserc.Mostrare che la metrica
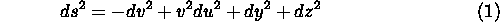
può essere ricondotta alla forma
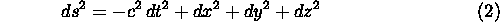
tramite un' opportuna trasformazione di coordinate.
Definizione ``intuitiva'' di spazio(tempo)curvo.
- 10-10-02: ``Coordinate Localmente Piatte''.
Eserc. Determinare un sitema di coordinate localmente
piatte su una sfera di raggio a, nell' intorno del punto di
coordinate 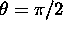 ,
, 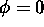 .
Trasfomazioni non-lineari tra sistemi di coordinate localmente piatte.
Utilità delle coordinate localmente piatte.
.
Trasfomazioni non-lineari tra sistemi di coordinate localmente piatte.
Utilità delle coordinate localmente piatte.
- 11-10-02: Linee Geodetiche. Lunghezza invariante di una curva
nello spazio(tempo).
Eserc. Ricavare l'equazione
delle geodetiche dalla condizione di stazionarietà:
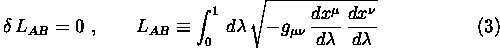
- 11-10-02: Invarianza per ri-parametrizzazioni di
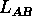 e forma canonica dell'equazioni delle geodetiche.
Geodetiche in coordinate localmente piatte.
e forma canonica dell'equazioni delle geodetiche.
Geodetiche in coordinate localmente piatte.
- 16-10-02: ``Parametri Affini''. ``L'ascensore
di Einstein''. Il ``peso'' come forza apparente.
Equivalenza tra sitemi di riferimento accelerati
uniformemente e campi gravitationali costanti.
- 16-10-02: Forze di marea.
Sistemi di riferimento localmente inerziali.
- 17-10-02: La `` Curvatura di Riemann'' e
la ``Curvatura di Ricci'' a confronto.
Vettori, Tensori e Forme differenziali
- 17-10-02: Manifold come modello geometrico dello spaziotempo.
Vettori controvarianti.
Spazio Tangente. Base di vettori nello Spazio
Tangente.
- 18-10-02: Base Naturale, o Base di Coordinate.
Trasformazioni di coordinate nel manifold e trasformazioni di base
nello spazio tangente.
- 18-10-02: 1-forme, definizione e proprità.
Spazio Co-tangente. Prodotto Scalare tra una 1-forma ed
un vettore. Base Naturale di 1-forme. Differenziale
di un funzione.
- 23-10-02: Tensori, definizione e proprità.
Base per un tensore tipo (r,s). Componenti covarianti
e controvarianti.
Legge di trasformazione delle componenti di un tensore, per
trasformazioni di base in
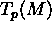 e
e 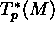 . Saturazione
di un indice covariante e di un indice controvariante.
. Saturazione
di un indice covariante e di un indice controvariante.
- 23-10-02:
Eserc. Dimostrare che
la saturazione di un indice covariante e di un indice controvariante
non dipende dalla scelta della base.
Parte simmetrica e parte antisimmetrica di un tensore.
p-forme.
- 24-10-02: Prodotto Esterno di p-forme. Base di
p-forme.
Eserc.Come si trasforma 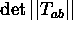 ?
Densità Tensoriali.
?
Densità Tensoriali.
Eserc.Dimostrare che nello spazio(tempo) di Minkowski
esiste un unico ``Simbolo di Levi-Civita''
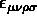 totalmente anti-simmetrico in tutti e
quattro gli indici.
totalmente anti-simmetrico in tutti e
quattro gli indici.
- 24-10-02:
Eserc. Dimostrare che il Simbolo di
Levi-Civita è una Densità tensoriale per trasformazioni
di coordinate.
Costruire il Tensore di Levi-Civita.
Costruire un elemento di volume invariante per trasformazioni
di coordinate.
- 25-10-02: La metrica e la sua inversa. Corrispondenza tra
componenti controvarianti e componenti covarianti.
Eserc.Come si può definire il ``tensore
controvariante di Levi-Civita '' ?
Quanto vale
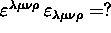 in 4 dimensioni?
in 4 dimensioni?
- 25-10-02: Definizione di Campo Tensoriale. La
Derivata Esterna di una p-forma: definizione e
proprietà formali.
Eserc. Dimostrare che 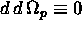 per ogni p-forma
per ogni p-forma 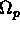 .
.
Costruire una rappresentazione grafica per il
differenziale 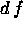 di una funzione f;
di una funzione f;
Costruire una rappresentazione grafica per le 1-forme della
base naturale 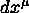 .
.
- 30-10-02:
Eserc.Si consideri un campo magnetico
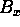 lungo la direzione x.
lungo la direzione x.
i) Ricavare le componenti del tensore (controvariante)
elettromagnetico corrisponente;
ii)Ricavare le componenti della 2-forma F corrispondente;
iii) Dare una rappresentazione grafica della 2-forma di cui al
punto ii);
iv) Si consideri una carica in moto con velcità 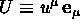 nel campo
nel campo 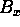 . Calcolare il prodotto
scalare
. Calcolare il prodotto
scalare  .
.
- 30-10-02:
Eserc. Dimostrare che le equazioni 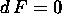 :
:
i) scritte in componenti diventano 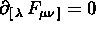 ;
;
ii) implicano l'esitenza di una 1-forma potenziale A: 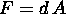 , e
che in componenti questo significa
, e
che in componenti questo significa
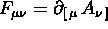 , e che la 1-forma
potenziale A è definita ``a meno di una 1-forma di gauge
, e che la 1-forma
potenziale A è definita ``a meno di una 1-forma di gauge
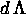 ;
;
Duale di Hodge di una p-forma.
- 31-10-02:
Eserc. Ricavare come si passa dalle
componenti di 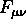 alle componenti del suo duale
alle componenti del suo duale
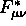 .
.
Definizione e propietà della derivata esterna aggiunta, o
co-derivata esterna, 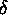 .
.
- 31-10-02:
Eserc.Dimostrare che le equazioni
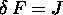 , con J 1-forma di corrente, in componenti danno
, con J 1-forma di corrente, in componenti danno
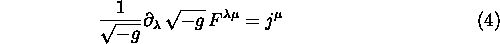
L' accopiamento tra la 1-forma potenziale A e la corrente J
è descritto geometricamente dal prodotto scalare 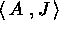 . Mantenendo fisso questo tipo di accoppiamento, costruire
la p-forma
. Mantenendo fisso questo tipo di accoppiamento, costruire
la p-forma 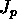 che si accoppia alla p-forma potenziale
che si accoppia alla p-forma potenziale 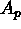 e descriverne il significato geometrico.
e descriverne il significato geometrico.
- 6-11-02:
Eserc. Il Teorema di Stokes
ammette una formulazione del tutto generale come:
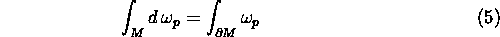
Considerare il caso 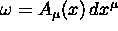 e
e 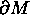 è una curva spaziale chiusa;
è una curva spaziale chiusa;
Considerare il caso 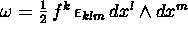 , e
, e 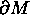 è una superficie chiusa.
è una superficie chiusa.
- 6-11-02: Base Ortonormale.
Eserc. Si consideri l'elemento di linea di una
2-sfera 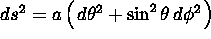 .
Determinare:
.
Determinare:
i) la base naturale in 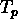 e
e 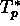 ;
;
ii)la base ortonormale in 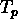 e
e 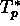 ;
La vierbein
;
La vierbein 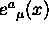 . Relazione tra vierbein e tensore
metrico.
. Relazione tra vierbein e tensore
metrico.
Coefficienti di Rotazione di Ricci.
- 6-11-02: Proprietà di trasfomazione di
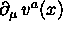 .
Simboli di Connessione. Derivata Covariante di un
vettore.
.
Simboli di Connessione. Derivata Covariante di un
vettore.
- 7-11-02: Proprietà di trasformazione della connessione, e della
derivata covariante, per ``rotazioni locali'' della base.
Derivata Covariante di una 1-forma.
- 7-11-02:Derivata Covariante di un tensore tipo (r,s)
- 7-11-02: Connessione in una base di coordinate.
Connessione e campi di forze inerziali.
- 8-11-02: Definizione di campo vettoriale (tensoriale)
Costante in senso Covariante.
Trasporto Parallelo di un vettore lungo una curva.
Curve auto-parallele. La Connessione di Christoffel.
- 8-11-02: Proprietà di auto-parallelismo delle geodetiche.
4-Accelerazione Covariante. Geodetiche, auto-parallele,e moto
``libero'' in uno spazio(tempo) curvo. Conservazione del modulo
di un 4-vettore per trasporto parallelo e condizioni di
Compatibilità tra metrica e connessione.
Eserc. Dimostrare che la connessione
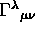 che soddisfa la condizione di
Compatibilità
che soddisfa la condizione di
Compatibilità
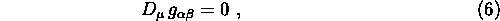
ed è simmetrica negli indici covarianti, in una Base di Coordinate,
i.e.
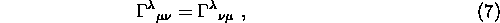
è la Connessione di Christoffel.
- 13-11-02: Limite classico dell'equazioni delle geodetiche.
Red-Shift gravitazionale.
- 13-11-02:
Eserc.Dimostrare che il Simbolo
di Christoffel, nella base naturale, si trasforma come una connessione
per trasformazioni generali di coordinate.
Ricavare l'espressione delle coordinate localmente inerziali
in termini di un sistema di coordinate dato e della connessione.
Dimostrare che se la metrica è diagonale, in una base di coordinate,
allora:
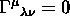 se
se 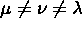 ;
;
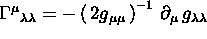 ;
;
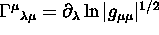 .
.
- 14-11-02:
Eserc. Dimostrare che se
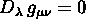 , anche
, anche 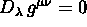 .
.
Dimostrare che 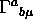 ha una parte anti-simmetrica
nella base ortonormale.
ha una parte anti-simmetrica
nella base ortonormale.
Dimostrare che
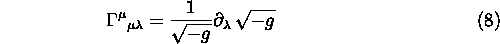
Ricavare la forma esplicita, in una base naturale,
per la divergenza covariante di:
un vettore controvariante;
un tensore controvariante a due indici;
un tensore controvariante a due indici anti-simmetrico.
Dimostrare che in una base naturale il rotore covariante di
un vettore covariante mantiene la sua forma ordinaria.
- 14-11-02:
Eserc. Scrivere la forma covariante
del tensore eletromagnetico, in termini del potenziale vettore 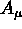 ,
e mostrare che mantiene la sua forma standard in una base naturale;
dimostrare che le Identitdi Bianchi per
,
e mostrare che mantiene la sua forma standard in una base naturale;
dimostrare che le Identitdi Bianchi per 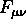 mantengono la
forma standard in una base naturale.
mantengono la
forma standard in una base naturale.
Ricavare la forma covariante generale dell' equazione d'onda per:
un campo scalare 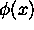 ;
un campo vettoriale
;
un campo vettoriale 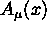 .
Principio di Covarianza Generale
.
Principio di Covarianza Generale
- 15-11-02: Trasporto parallelo di una base
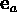 lungo un
percorso chiuso. Curvatura della Connessione e Tensore
di Riemann-Christoffel.
lungo un
percorso chiuso. Curvatura della Connessione e Tensore
di Riemann-Christoffel.
Eserc. Dimostrare che:
le matrici 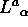 di trasformazione di base in
di trasformazione di base in 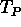 soddisfano la condizione
soddisfano la condizione 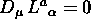 ;
;
Dimostrare che:
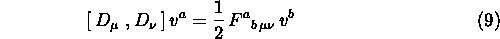
dimostrare che 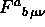 si trasforma come un
tensore.
si trasforma come un
tensore.
- 15-11-02:
Eserc. Dimostrare che:
se 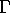 è una ``Connessione Piatta'', i.e.
è una ``Connessione Piatta'', i.e.
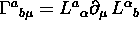 ,
la corrispondente curvatura è zero;
,
la corrispondente curvatura è zero;
se 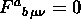 , allora esiste una matrice
di trasformazione
, allora esiste una matrice
di trasformazione 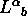 che permette di scrivere la metrica
in forma piatta dovunque.
che permette di scrivere la metrica
in forma piatta dovunque.
Calcolare il ``Limite Classico'' del Tensore di
Riemann-Christoffel.
- 20-11-02:
Eserc.Calcolare le componenti del tensore di
Riemann-Christoffel, per una sfera; da questo risultato
ricavare una ``curvatura scalare'' .
Si consideri il vettore 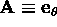 nel
punto
nel
punto 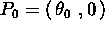 . Calcolare le componenti
ed il modulo del vettore
. Calcolare le componenti
ed il modulo del vettore 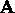 trasportato parallelo lungo
la linea
trasportato parallelo lungo
la linea 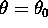 .
.
- 20-11-02:Identità di Bianchi.Tensore e
Scalare di Ricci. Derivazione euristica delle Equazioni di Campo
di Einstein.
- 21-11-02:
Eserc.Dimostrare che:
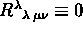 ;
; 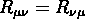
Limite classico delle equazioni di campo di Einstein.
- 21-11-02:
Eserc.Analisi dimensionale delle equazioni di campo di
Einstein. Limiti di applicabilità della Teoria della Relatività
Generale. Il termine cosmologico.
- 22-11-02:
Definizione euristica del Tensore Energia-Impulso come
``corrente del 4-vettore energia-impulso''.
Eserc.Costruire il Tensore Energia-Impulso per
una particella puntiforme;
mostrare che se non ci sono forze esterne, allora
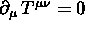 in un sistema di coordinate localmente
inerziali;
in un sistema di coordinate localmente
inerziali;
mostrare che in un sistema di riferimento generico che, se
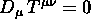 allora la particella si muove lungo una
geodetica.
allora la particella si muove lungo una
geodetica.
- 22-11-02:
Tensore Energia-Impulso di un fluido perfetto.
Tensore Energia-Impulso del vuoto e la Costante Cosmologica.



Next: About this document
Euro Spallucci
Wed Jul 24 13:39:51 MET DST 2002