... Shells¹

To appear in the Proceedings of the 6th International Symposium on Frontiers in Fundamental and Computational Physics (FFP6), September 26-29, Udine, ITALY

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... Ansoldi²

Email: ansoldi@trieste.infn.it

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... Ansoldi^2 3

Webpage: http://www-dft.ts.infn.it/$\sim$ansoldi

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... Sindoni⁴

Email: potenzo17@yahoo.it

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... equation⁵

Following a standard notation, quantities in the two spacetime regions separated by the shell are identified by 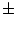$\pm$ subscripts. We use square brackets ``$[\dots{}]$'' to denote their jump in going from the ``$-$'' to the ``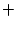$+$'' side of the shell and an overdot, ``$\dot{\quad}$'', to indicate the derivative with respect to the proper time measured by a shell-comoving observer.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... trajectory⁶

Our formulation here is far too synthetic and we refer the reader to the literature on the subject (for example [5,6]) for extended background material.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... means⁷

This is a strong argument in favor of an expression for the effective momentum that, when evaluated along a classically forbidden trajectory, differs from (2), also evaluated on a classically forbidden trajectory, by a total derivative of a function of 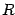$R$, at most.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.