|
|
|
| Education: |
| Details about attended postgraduate
courses during the PhD: |
|
| |
|
|
| |
|
ALGEBRAIC QUANTUM THEORY, FIELD
THEORY AND STATISTICAL MECHANICS (Prof. G. Sewell, University of London): |
|
| |
|
|
Introduction to Algebraic Quantum Field
Theory and its Relations with More Traditional Approaches to Quantum Field
Theory; From Finite Systems to Infinite Systems: Von Neumann Theorem; Algebraic
Interlude: Algebras, *-Algebras, Normed Algebras, 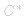 -Algebras,
States, GNS Representation, -Algebras,
States, GNS Representation, 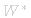 -Algebras
and their Properties, Normal Functionals; Examples of Infinite Systems,
Definition of Dynamics, Macroscopic Observables and Primary Fields; Lattice
Systems: Explicit Construction; Continuous Systems: Explicit Construction;
Local and Global Structures; the Algebra of Observables; KMS Condition and
KMS States; Application to Relativistic Field Theories; -Algebras
and their Properties, Normal Functionals; Examples of Infinite Systems,
Definition of Dynamics, Macroscopic Observables and Primary Fields; Lattice
Systems: Explicit Construction; Continuous Systems: Explicit Construction;
Local and Global Structures; the Algebra of Observables; KMS Condition and
KMS States; Application to Relativistic Field Theories; |
|
| |
|
End course seminar given:
Quantum Theory of Measurement and Macroscopic Observables; |
|
| |
|
BASICS OF COSMOPARTICLE PHYSICS
(Prof. Y. Khlopov, University of Moscow): |
|
| |
|
|
CosmoParticle Physics: Basic Laws,
Interrelations between Physical, Astrophysical and Cosmological Quantities;
the Framework of the Theory of Everything; New standards in Big Bang Cosmology;
Inflation, Baryosinthesis, Density Fluctuations in the Primordial Universe;
Dark Matter; CosmoArcheology; Topological Defects. |
|
| |
|
QUANTUM THEORY (Prof. R. Iengo,
S.I.S.S.A. - Trieste - Italy): |
|
| |
|
|
Path Integral Formalism; Relations
between the Canonical Quantization Procedure and the Path Integral One;
Regularization; Renormalization of
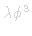 and and
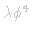 Theories; Renormalization of Gauge Theories: Renormalization
of QED, Renormalization of QCD; Ward Identities; Anomalies; Renormalization
of Composite Operators; Deep Inelastic Scattering. Theories; Renormalization of Gauge Theories: Renormalization
of QED, Renormalization of QCD; Ward Identities; Anomalies; Renormalization
of Composite Operators; Deep Inelastic Scattering. |
|
| |
|
SOLITONS AND INSTANTONS (Prof.
R. Percacci, S.I.S.S.A. - Trieste - Italy): |
|
| |
|
|
Topology and Physics, an Introduction
to Topology, Homotopy, Homology, Cohomology, Group Actions on Manifold and
the Local Geometry and Topology of Spaces of Maps; Solitons in low Dimensions;
Linear and Non-Linear Scalar Fields in Higher Dimensions; Nonlinear Sigma
Models; Current Algebra and Skyrmions; Solitons in Yang-Mills Theories;
the Nielsen-Olesen Vortex; the 't Hooft-Polyakov Monopole; the Aharonov
Bohm Effect; Theta Sectors; Path Integrals and Instantons; the Dirac Quantization
Condition; Wess-Zumino-Witten Terms; Chern-Simons Terms; |
|
| |
|
End course seminar given:
Finkelstein-Misner Kinks and Topological Effects in Gravity Theories. |
|
| |
|
QUANTUM FIELD THEORY II
(Prof. J.Flynn, Department of Physics and Astronomy
of the University of Southampton - Southampton - UK): |
|
| |
|
|
Quantisation of the Free ElectroMagnetic
Field, Feynman Rules for QED, tree level process in QED; Euclidean Theory,
Wick Rotation, Effective Action, 1PI functions,
self-energy and two point function, Classical Action as tree diagrams generator,
Dyson-Schwinger equations, Symmetry and Noether Theorem; Ward
identities; Feynman diagrams, power counting, renormalizability, regularization;
one-loop computations, counterterms, bare and renormalized lagrangians,
multiplicative renormalization, rrenormalization conditions; renormalization
conditions, beta function, Landau pole, asymptotic freedom, fixed points;
Gauge Invariance, zero modes and Fadddeev-Popov procedure in QED, one loop
divergencies, Ward identity, vertex corrections and anomalous magnetic moment;
non-abelian gauge theories and Faddeev-Popov trick in non-abelian gauge
theories, ghosts, Feynman rules and renormalizability in the non-abelian
case; Slavnov-Taylor identities, beta function for QCD and asymptotic freedom;
Goldstone theorem (classical), Fabri-Picasso theorem, Goldstone theorem
(quantum), Higgs mechanism, Unitary gauge, renormalizable gauges; Standard
Model. |
|
| |
|
CONTINUOUS DYNAMICAL SYSTEMS
(Prof. C.J.S.Clarke, Department of Mathematics of
the University of Southampton - Southampton - UK): |
|
| |
|
|
Introduction and Examples, phase diagrams,
discrete and continuous linear systems, comparison theorems, linear systems,
phase space analysis, periodic solutions and limit cycles, hamiltonian dynamical
systems, relations between continuous and discrete dinamical systems, stability. |
|
| |
PhD Thesis: |
|
| |
|
Title:
Boundary versus Bulk Dynamics of Extended Objects and the Fractal
Structure of Quantum Spacetime; |
|
| |
|
Tutor:
Prof. Tullio Weber; |
|
| |
|
CoTutor:
Dr. Euro Spallucci. |
|
|
 |
|
|
|