We concentrate in this appendix on the computation of the contribution
![]() of equation (28). Of
course since the integral is divergent, it must be properly
regularized and we choose to do that by putting an infrared
(
of equation (28). Of
course since the integral is divergent, it must be properly
regularized and we choose to do that by putting an infrared
(![]() ) and an ultraviolet (
) and an ultraviolet (![]() ) cutoff on the modulus of
the momentum
) cutoff on the modulus of
the momentum ![]() and of its projection
and of its projection ![]() , exploiting some of
the arbitrariness in the choice of the regularization scheme. Thus
integrals written with implicit integration domain, like
, exploiting some of
the arbitrariness in the choice of the regularization scheme. Thus
integrals written with implicit integration domain, like
![]() , are to be understood as performed in the domain of the
variables
, are to be understood as performed in the domain of the
variables
![]() , which is the inverse
image of the domain
, which is the inverse
image of the domain
![]() ,
,
![]() ,
,
![]() ,
,
![]() in the variables
in the variables
![]() under the following
change of variables in euclidean space:
under the following
change of variables in euclidean space:
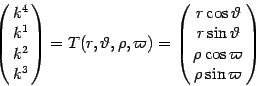
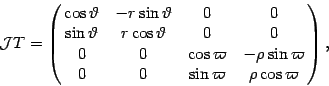
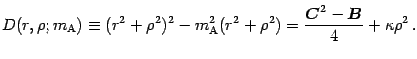 |