

Next: B. Determination of the
Up: RealImaginaryMass
Previous: Acknowledgments
A. Eigenvectors and
eigenvalues of the propagator
We will now find the solutions to the eigenvector equation
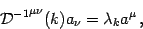 |
(34) |
where
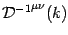 is defined in
equation (21).
is defined in
equation (21).
Firstly, there is a ``trivial'' gauge solution
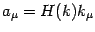 , since
, since 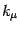 is orthogonal to both terms enclosed in round
brackets in the definition (21) of
is orthogonal to both terms enclosed in round
brackets in the definition (21) of
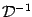 ;
this can be seen from the relations
;
this can be seen from the relations
and
using the properties
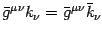 and
and
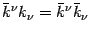 .
.
A second, non trivial polarization is
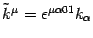 in the electric case (
in the electric case (
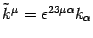 in the magnetic case), since
in the magnetic case), since
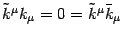 thanks to equations (19)
and (20);
thanks to equations (19)
and (20);
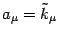 is
associated to the eigenvalue
is
associated to the eigenvalue
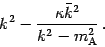 |
(35) |
Then, remaining independent physically relevant polarizations must be
orthogonal to both 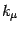 and
and
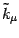 , hence they can
be parametrized as
, hence they can
be parametrized as
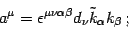 |
(36) |
since 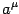 given by (36) is not affected by the
``gauge transformation''
given by (36) is not affected by the
``gauge transformation''
it then follows that only two components of 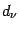 are physically
relevant. One of these, which we will call
are physically
relevant. One of these, which we will call
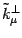 , is obtained when
, is obtained when
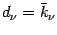 : it is thus
orthogonal to
: it is thus
orthogonal to 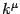 ,
,
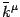 ,
,
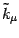 and
corresponds to the eigenvalue
and
corresponds to the eigenvalue 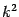 . This is the same eigenvalue of
the last eigenvector,
. This is the same eigenvalue of
the last eigenvector, 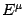 , which is given by
, which is given by
This can be verified by inserting it
into (18) and observing that
The above equality holds because
is a projector onto the space orthogonal to
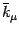 in
the
in
the 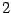 -dimensional subspace, where the direction orthogonal to
-dimensional subspace, where the direction orthogonal to
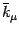 is nothing but
is nothing but
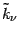 .
.


Next: B. Determination of the
Up: RealImaginaryMass
Previous: Acknowledgments
Stefano Ansoldi
![]() , since
, since ![]() is orthogonal to both terms enclosed in round
brackets in the definition (21) of
is orthogonal to both terms enclosed in round
brackets in the definition (21) of
![]() ;
this can be seen from the relations
;
this can be seen from the relations
![]() in the electric case (
in the electric case (
![]() in the magnetic case), since
in the magnetic case), since
![]() thanks to equations (19)
and (20);
thanks to equations (19)
and (20);
![]() is
associated to the eigenvalue
is
associated to the eigenvalue
![]() and
and
![]() , hence they can
be parametrized as
, hence they can
be parametrized as