Equipped with the formalism developed in the previous sections,
we now wish to consider the extension
of the path-integral method to the case of open ![]() -branes. As we
shall see, the main
difference stems from the fact that a gauge invariant action for an
open
-branes. As we
shall see, the main
difference stems from the fact that a gauge invariant action for an
open ![]() -brane requires the introduction of new gauge fields to
compensate for the gauge symmetry ``leakage'' through the boundary
[11]. Thus, we replace the system (57-58)
with the following one,
-brane requires the introduction of new gauge fields to
compensate for the gauge symmetry ``leakage'' through the boundary
[11]. Thus, we replace the system (57-58)
with the following one,
![$\displaystyle {1 \over Z [ \, 0 \, ]}
\int [ {\mathcal{D}}A ] [ {\mathcal{D}}C ]
\,
e ^{ - S [ \, A , C , J _{\mathrm{e}} \, ]}$](img119.gif) |
|||
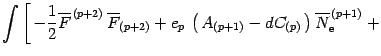 |
|||
| (91) |
| (92) |
| (93) | |||
| (94) |
| (95) |
![$\displaystyle \int [ {\mathcal{D}}D ]
e ^ {\imath\, S [ \, D\ , \Theta \, ] }$](img276.gif) |
(96) | ||
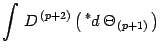 |
|||
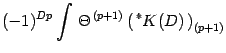 |
(97) | ||
| (98) |
| (99) |
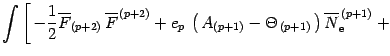 |
|||
| (100) |
| (101) |
| (102) |
with
| (104) |
>From the dual action (105) one gets the field equations
Solving equation (107) one finds
After decomposing the magnetic parent current as
| (110) |
equation (108) becomes
and gives for
![]() the following solution
the following solution
When (112), (113) are inserted back into (105)
we find
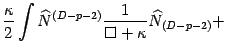 |
|||
![$\displaystyle \int \left[\, { g_{D-p-4 \, }^2\over 2 }
\overline{J} _{\mathrm{g...
... \kappa} j _{\mathrm{e}} ^{\,(p)}
{ 1\over \Box } j _{\mathrm{e}\,(p)}\,\right]$](img311.gif) |
(114) |
where, short-range bulk and long range boundary interaction are clearly displayed.
|
Spacetime
manifold |
Embedding
functions |
Fiducial
manifold |
Parameters
|
Source
Current |
Dimensionality
|
|
| Type | ||||||
| Electric | ||||||
| Magnetic | ||||||
|
Magnetic
Dirac brane |
||||||
|
Electric
Dirac brane |
|
|
|
|||
| Table 1: Definition of electric/magnetic objects. | ||||||
dual-brane |
||||
| 0 | point-particle | 7-brane | ||
| 1 | string | 6-brane | ||
| 2 | membrane | 5-brane | ||
| 3 | bag | 4-brane | ||
| Table 2: Closed |
||||
| Field | Dimension in |
Rank | Physical Meaning |
|
|
|
``electric'' potential | |
|
|
|
``electric'' field strength | |
|
|
|
``magnetic'' field strength | |
|
|
|
``singular'' field strength | |
|
|
|
dual gauge potential | |
|
|
|
dual field strength | |
| Table 3: Closed |
|||
| Current Density | Dimension in |
Rank | Physical Meaning |
|
|
|
electric current | |
|
|
|
parent electric current | |
|
|
|
magnetic current | |
|
|
|
parent magnetic current | |
|
|
|
gauge brane current | |
| Table 4: Closed |
|||
| Field | Dimension in |
Rank | Physical Meaning |
|
|
|
``electric'' potential | |
|
|
|
``electric'' field strength | |
|
|
|
Stückelberg gauge potential | |
|
|
|
Stückelberg field strength | |
|
|
|
dual Stückelberg potential | |
|
|
|
dual Stückelberg strength | |
|
Table 5: Open
|
|||
| Current Density | Dimension in |
Rank | Physical Meaning |
|
|
|
electric parent current | |
|
|
|
boundary current | |
|
|
|
parent magnetic current | |
|
|
|
magnetic current | |
|
Table 6: Open
|
|||
|
dual-brane |
||
| point-particle | ||
| string | ||
| membrane | ||
| bag | ||
| Table 8: Open |
||