To get some analytical result we try to fit the ![]() points for which
we evaluated the action with some simple (polynomial) function. In this way we
will be able to get an (approximated) relation among
points for which
we evaluated the action with some simple (polynomial) function. In this way we
will be able to get an (approximated) relation among ![]() ,
, ![]() and
and ![]() .
The choice of the approximating function is done with two goals in mind:
.
The choice of the approximating function is done with two goals in mind:
 |
||
|
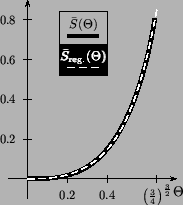
Figure: Comparison between approximated
and numerical evaluated actions. The expression
|
||
 |
||
|
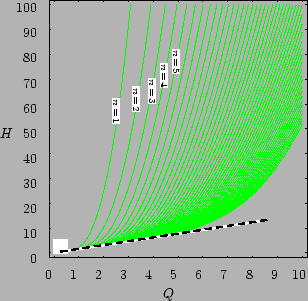
Figure 13: Graph of the level curves
for the approximated action levels
|
||
From the approximated expression (27), which
by (25) and (26) must equal ![]() when
multiplied by
when
multiplied by ![]() , we can get the following equation
of the third degree in H,
, we can get the following equation
of the third degree in H,