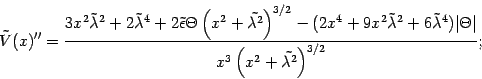 |
(35) |
With the above results at hand, we now evaluate the second derivative of the
effective potential, i.e.
Even with the above simplification, the detailed study of the sign of the quantity under
consideration is complicated, mainly because of the non-trivial ![]() dependence;
a graphical analysis is also of little help, since
dependence;
a graphical analysis is also of little help, since
![]() depends on the three variables
depends on the three variables ![]() ,
,
![]() and
and
![]() ,
namely the adimensional charge
,
namely the adimensional charge ![]() , the charge/mass ratio
, the charge/mass ratio ![]() of the test particle
and the adimensional angular momentum per unit mass
of the test particle
and the adimensional angular momentum per unit mass ![]() of the test particle.
Thus we will not search for the most general result, i.e. we will not give
necessary and sufficient conditions for the stability of the shell;
we will show, instead, that in some physically reasonable situations the shell itself
is indeed stable against single charged particle decay.
of the test particle.
Thus we will not search for the most general result, i.e. we will not give
necessary and sufficient conditions for the stability of the shell;
we will show, instead, that in some physically reasonable situations the shell itself
is indeed stable against single charged particle decay.
In particular we see that in the units we are using, the adimensional parameter
![]() is a large number, i.e. the charge/mass ratio for an elementary
particle is very large. Thus we consider the behaviour of the numerator for large
is a large number, i.e. the charge/mass ratio for an elementary
particle is very large. Thus we consider the behaviour of the numerator for large
![]() :
:
As a second case, we see what happens for radial emission of particles:
Even restricting the study to the two cases above, we can thus conclude that, shell configurations which are stable against single particle decay can be realized.